9 releases
| 0.3.2 | Jan 7, 2025 |
|---|---|
| 0.3.1 | Sep 8, 2024 |
| 0.2.1 | Jul 24, 2024 |
| 0.1.3 | Jun 19, 2024 |
| 0.1.0 | Feb 25, 2024 |
#461 in Math
131 downloads per month
Used in icao-wgs84
91KB
1.5K
SLoC
unit-sphere
A library for performing geometric calculations on the surface of a sphere.
The library uses a combination of spherical trigonometry and vector geometry to perform great-circle navigation on the surface of a unit sphere, see Figure 1.
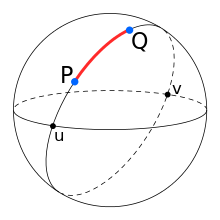 Figure 1 A Great Circle Path
Figure 1 A Great Circle Path
A great circle is the shortest path between positions on the surface of a sphere. It is the spherical equivalent of a straight line in planar geometry.
Spherical trigonometry
A great circle path between positions may be calculated using spherical trigonometry.
The course
(initial azimuth) of a great circle can be calculated from the
latitudes and longitudes of the start and end points.
While great circle distance can also be calculated from the latitudes and
longitudes of the start and end points using the
haversine formula.
The resulting distance in Radians can be converted to the required units by multiplying the distance by the Earth radius measured in the required units.
Vector geometry
Points on the surface of a sphere and great circle poles may be represented by 3D vectors. Many calculations are simpler using vectors than spherical trigonometry.
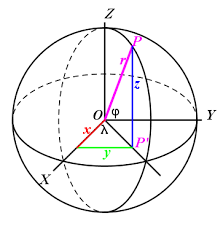 Figure 2 Spherical Vector Coordinates
Figure 2 Spherical Vector Coordinates
For example, the across track distance of a point from a great circle can be calculated from the dot product of the point and the great circle pole vectors. While the intersection points of great circles can simply be calculated from the cross product of their pole vectors.
Design
The great_circle module performs spherical trigonometric calculations
and the vector module performs vector geometry calculations.
The library is declared no_std so it can be used in embedded applications.
Example
The following example calculates the intersection between two Great Circle Arcs.
The values are taken from Charles Karney's original solution to
Intersection between two geodesic lines.
use unit_sphere::{Arc, Degrees, LatLong, calculate_intersection_point};
use angle_sc::is_within_tolerance;
let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));
let accra = LatLong::new(Degrees(6.0), Degrees(0.0));
let arc1 = Arc::try_from((&istanbul, &washington)).unwrap();
let arc2 = Arc::try_from((&reyjavik, &accra)).unwrap();
let intersection_point = calculate_intersection_point(&arc1, &arc2).unwrap();
let lat_long = LatLong::from(&intersection_point);
// Geodesic intersection latitude is 54.7170296089477
assert!(is_within_tolerance(54.72, lat_long.lat().0, 0.05));
// Geodesic intersection longitude is -14.56385574430775
assert!(is_within_tolerance(-14.56, lat_long.lon().0, 0.02));
Contribution
If you want to contribute through code or documentation, the Contributing guide is the best place to start. If you have any questions, please feel free to ask. Just please abide by our Code of Conduct.
License
unit-sphere is provided under a MIT license, see LICENSE.
Dependencies
~4.5MB
~94K SLoC