1 unstable release
Uses new Rust 2024
| 0.1.0 | Mar 23, 2025 |
|---|
#372 in Math
129 downloads per month
490KB
3K
SLoC

rgode is a Rust library for solving ordinary differential equations (ODEs). The library provides a set of numerical methods and solout implementations for solving initial value problems (IVPs). The library is designed to be easy to use, flexible, and efficient for solving a wide range of ODEs.
Table of Contents
- Solvers
- Defining a System
- Solving an Initial Value Problem (IVP)
- Examples
- Installation
- Notation
- Running Tests
- Citation
- References
Solvers
The library includes a set of solvers for solving ODEs. The solver algorithmic core and coefficients are implemented as structs implementing the Solver trait. The solver's settings can then be configured before being used in the ivp.solve(&mut solver) method which acts as the controller for the solver. Note that due to this design, the solvers are not literal translations but the algorithmic core and coefficients are the same.
Fixed Step Size
| Solver | Description |
|---|---|
Euler |
Euler's method (1st order Runge-Kutta) |
Midpoint |
Midpoint method (2nd order Runge-Kutta) |
Heuns |
Heun's method (2nd order Runge-Kutta) |
Ralston |
Ralston's method (2nd order Runge-Kutta) |
RK4 |
Classical 4th order Runge-Kutta method |
ThreeEights |
3/8 Rule 4th order Runge-Kutta method |
APCF4 |
Adams-Predictor-Corrector 4th order fixed step-size method |
Adaptive Step Size
| Solver | Description |
|---|---|
RKF |
Runge-Kutta-Fehlberg 4(5) adaptive method |
CashKarp |
Cash-Karp 4(5) adaptive method |
DOPRI5 |
Dormand-Prince 5(4) adaptive method |
DOP853 |
Explicit Runge-Kutta method of order 8 |
APCV4 |
Adams-Predictor-Corrector 4th order variable step-size method |
All solvers except DOP853, which has its own higher-order internal interpolation method, uses cubic Hermite interpolation method for calculating desired t-out values and finding eventAction::Terminate points.
Defining a System
The System trait defines the differential equation dydt = f(t, y) for the solver. The differential equation is used to solve the ordinary differential equation. The trait also includes a event function to interrupt the solver when a condition is met or an event occurs.
System Trait
diff- Differential Equationdydt = f(t, y)in the formf(t, &y, &mut dydt).event- Optional event function to interrupt the solver when a condition is met by returningEventAction::Terminate(reason: EventData). Theeventfunction by default returnsEventAction::Continueand thus is ignored. Note thatEventDatais by default aStringbut can be replaced with anything implementingClone + Debug.
Solout Trait
solout- function to choose which points to save in the solution. This is useful when you want to save only points that meet certain criteria. Common implementations are included in thesoloutmodule. TheIVPtrait implements methods to use them easily without direct interaction as well e.g.even,dense, andt_eval.
Implementation
// Includes required elements and common solvers.
// Less common solvers are in the `solvers` module
// Also re-exports nalgebra SVector type and vector! macro
use rgode::prelude::*;
struct LogisticGrowth {
k: f64,
m: f64,
}
impl System<f64, 1, 1> for LogisticGrowth {
fn diff(&self, _t: f64, y: &SVector<f64, 1>, dydt: &mut SVector<f64, 1>) {
dydt[0] = self.k * y[0] * (1.0 - y[0] / self.m);
}
fn event(&self, _t: f64, y: &SVector<f64, 1>, _dydt: &SVector<f64, 1>) -> EventAction {
if y[0] > 0.9 * self.m {
EventAction::Terminate("Reached 90% of carrying capacity".to_string())
} else {
EventAction::Continue
}
}
}
Note that for clarity, the System is defined with generics <f64, 1, 1> where f64 is the float type and 1, 1 is the dimension of the system of ordinary differential equations. By default the generics are f64, 1, 1 and thus can be omitted if the system is a single ODE with a f64 type.
Solving an Initial Value Problem (IVP)
The IVP trait is used to solve the system using the solver. The trait includes methods to set the initial conditions, solve the system, and get the solution. The solve method returns a Result<Solution, SolverStatus> where Solution is a struct containing the solution including fields with outputted t, y, and the solver status, and SolverStatus is returned with the error if it occurs. In addition, statistics including steps, evals, rejected steps, accepted steps, and the solve time are included as fields in the Solution struct.
fn main() {
let mut solver = DOP853::new().rtol(1e-12).atol(1e-12);
let y0 = vector![1.0];
let t0 = 0.0;
let tf = 10.0;
let system = LogisticGrowth { k: 1.0, m: 10.0 };
let logistic_growth_ivp = IVP::new(system, t0, tf, y0);
match logistic_growth_ivp
.even(1.0) // uses TEvalSolout to save with dt of 1.0
.solve(&mut solver) // Solve the system and return the solution
{
Ok(solution) => {
// Check if the solver stopped due to the event command
if let SolverStatus::Interrupted(ref reason) = solution.status {
// State the reason why the solver stopped
println!("Solver stopped: {}", reason);
}
// Print the solution
println!("Solution:");
for (t, y) in solution.iter() {
println!("({:.4}, {:.4})", t, y[0]);
}
// Print the statistics
println!("Function evaluations: {}", solution.evals);
println!("Steps: {}", solution.steps);
println!("Rejected Steps: {}", solution.rejected_steps);
println!("Accepted Steps: {}", solution.accepted_steps);
}
Err(e) => panic!("Error: {:?}", e),
};
}
Output
Solver stopped: Reached 90% of carrying capacity
Solution:
(0.0000, 1.0000)
(1.0000, 2.3197)
(2.0000, 4.5085)
(3.0000, 6.9057)
(4.0000, 8.5849)
(4.3944, 9.0000)
Function evaluations: 359
Steps: 25
Rejected Steps: 4
Accepted Steps: 25
Examples
For more examples, see the examples directory. The examples demonstrate different systems, solvers, and output methods for different use cases.
| Example | Description & Demonstrated Features |
|---|---|
| Exponential Growth | Solves a simple exponential growth equation using the DOP853 solver. Demonstrates basic usage of IVP and System traits. Manually prints results from Solution struct fields. |
| Harmonic Oscillator | Simulates a harmonic oscillator system using RK4 method. Uses a condensed setup to demonstrate chaining to solve without intermediate variables. Uses last method on solution to conveniently get results and print. |
| Logistic Growth | Models logistic growth with a carrying capacity. Demonstrates the use of the event function to stop the solver based on a condition. In addition shows the use of even output for IVP setup and iter method on the solution for output. |
| SIR Model | Simulates the SIR model for infectious diseases. Uses the APCV4 solver to solve the system. Uses custom event termination enum. |
| Damped Pendulum | Simulates a simple pendulum using the RKF solver. Shows the use of ivp.t_out to define points to be saved e.g. t_eval = [1.0, 3.0, 7.5, 10.0] |
| Integration | Demonstrates the differences between even, dense, t_out, and the default solout methods for a simple differential equation with an easily found analytical solution. |
| Cr3bp | Simulates the Circular Restricted Three-Body Problem (CR3BP) using the DOP853 solver. Uses the hyperplane_crossing method to log when the spacecraft crosses a 3D plane. |
| Damped Oscillator | Demonstrates the use of the crossing method to use the CrossingSolout to log instances where a crossing occurs. In this case, the example saves points where the position is at zero. |
| Matrix System | Solves a system of ODEs using a matrix system. Demonstrates how to define a system of equations using matrices. |
| Custom Solout | Demonstrates how to create a custom Solout implementation to save points based on a custom condition. In addition inside the Solout struct additional calculations are stored and then accessed via Solution.solout.(fields) |
Installation
To use rgode in your Rust project, add it as a dependency using cargo:
cargo add rgode
Benchmarks
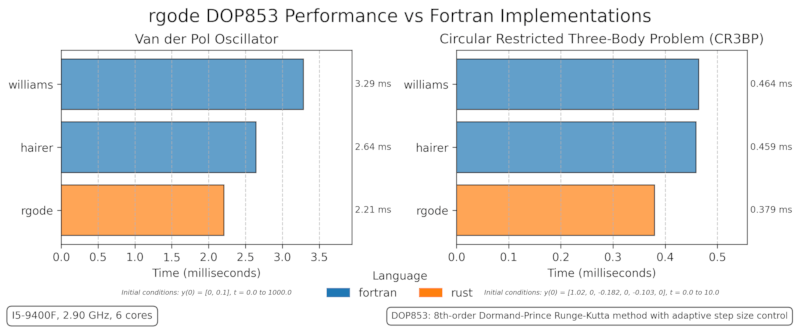
Included is a submodule rgode-benchmarks which contains benchmarks comparing the speed of the DOP853 solver implementation in rgode against implementations in other programming languages including Fortran.
A sample result via rgode-benchmarks is shown below:
Testing has shown that the rgode Rust implementation is about 10% faster than the Fortran implementations above. Take the result with a grain of salt as more testing by other users is needed to confirm the results.
More information can be found in the rgode-benchmarks directory's README.
Notation
Typical ODE libraries either use x or t for the independent variable and y for the dependent variable. This library uses the following notation:
t- The independent variable, typically time oftenxin other ode libraries.y- The dependent variable, instead ofxto avoid confusion with an independent variable in other notations.dydt- The derivative ofywith respect tot.k- The coefficients of the solver, typically a derivative such as in the Runge-Kutta methods.
Any future solvers added to the library should follow this notation to maintain consistency.
Testing
The library includes a suite of tests to verify the accuracy of the solvers, check for edge cases, and ensure the library is functioning correctly. After cloning the repo you can run the tests by using the following command:
cargo test
Included in the /tests/ directory is some python scripts to compare against scipy's solve_ivp.
python ./tests/python_comparison/solve_ivp.py
python ./tests/python_comparison/plots.py
solve_ivp.py will run scipy's solve_ivp on the same systems as the tests, and are in fact used as the expected values in the rgode tests. plots.py will take all the CSV files generated from the tests and plot them together for a visual comparison.
Citation
If you use this library in your research, please consider citing it as follows:
@software{rgode,
author = {Ryan D. Gast},
title = {rgode: A Rust library for solving ordinary differential equations.},
url = {https://github.com/Ryan-D-Gast/rgode},
version = {0.1.0},
}
References
The following references were used in the development of this library:
- Burden, R.L. and Faires, J.D. (2010) Numerical Analysis. 9th Edition, Brooks/Cole, Cengage Learning, Boston.Burden, R. L., Faires, J. D.
- E. Hairer, S.P. Norsett and G. Wanner, "Solving ordinary Differential Equations I. Nonstiff Problems", 2nd edition. Springer Series in Computational Mathematics, Springer-Verlag (1993).
- Ernst Hairer's website: Fortran and Matlab Codes
Dependencies
~3–12MB
~149K SLoC