1 unstable release
Uses new Rust 2024
| 0.2.25 | Mar 19, 2025 |
|---|---|
| 0.2.23 |
|
| 0.2.16 |
|
| 0.2.10 |
|
#90 in Math
2,118 downloads per month
Used in kithe
4MB
17K
SLoC
[TOC]
RustedSciThe
is a Rust library for symbolic and numerical computing: parse string expressions in symbolic representation/symbolic function and compute symbolic derivatives or/and transform symbolic expressions into regular Rust functions, compute symbolic Jacobian and solve initial value problems for for stiff ODEs with BDF and Backward Euler methods, non-stiff ODEs and Boundary Value Problem (BVP) using Newton iterations. NOTE: Symbolic part of the crate is not supposed to be a "full-scale" all-purpose symbolic library even now it provides a descent amount of features it was supposed for the following main goals a) analytical Jacobians for differential equations b) pretty printing of custom equations c) convenient input of custom equations without the need to wrap the right-hand side function in the implementation of some structure, as is done in many crates, which is quite cumbersome.
PROJECT NEWS: analytical Taylor series added
ATTENTION: for those interested in solving BVP there is an in-depth guide for the part of the crate concerned with the BVP on github page of the project (in eng. and rus.). Find it in the Book folder.
Content
Motivation
At first, this code was part of the KiThe crate, where it was supposed to serve for constructing analytical Jacobians for solving systems of equations of combustion, chemical kinetics and heat and mass transfer, as well as for displaying analytical expressions, but it soon became clear that it could be useful for a broader circle of users
Features
- parsing string expressions in symbolic to a symbolic expression/function
- symbolic/analytical differentiation of symbolic expressions/functions
- compare analytical derivative to a numerical one
- calculate vector of partial derivatives
- transform symbolic expressions/functions (also derivatives) into regular Rust functions
- calculate symbolic/analytical Jacobian and transform it into functional form
- Newton-Raphson method with analytical Jacobian
- Backward Eeuler method with analytical Jacobian
- Backward Differetiation Formula method (BDF) with analytical Jacobian (direct rewrite of python BDF solver from SciPy library)
- classical methods for non-stiff equations RK45 and DP
- Boundary Value Problem for ODE with Newton-Raphson method (several versions available)
project_documentation
In the ‘Book’ folder of the project (on github) there is an in-depth scientific manual as well as a developer's and user's manual in English and Russian. So far a chapter on BVP solution has been added. The chapter is under development and may contain some errors and omissions.
The project folder ‘Examples’ contains working examples of code usage.
Usage
- parse string expression of multiple arguments to a symbolic representation/function and then differentiate it and "lamdufy" it (transform it into a regular rust function). Compare analytical derivative to a numerical one. Calculate the vector of partials derivatives. Solve IVP and BVP problems.
// FUNCTION OF MULTIPLE VARIABLES
//parse expression from string to symbolic expression
let input = "exp(_x)+log(_y)";
// here you've got symbolic expression
let parsed_expression = Expr::parse_expression(input);
println!(" parsed_expression {}", parsed_expression);
// turn symbolic expression to a pretty human-readable string
let parsed_function = parsed_expression.sym_to_str("_x");
println!("{}, sym to string: {} \n",input, parsed_function);
// return _vec of all arguments
let all = parsed_expression.all_arguments_are_variables();
println!("all arguments are variables {:?}",all);
let variables = parsed_expression.extract_variables();
println!("variables {:?}",variables);
// differentiate with respect to _x and _y
let df_dx = parsed_expression.diff("_x");
let df_dy = parsed_expression.diff("_y");
println!("df_dx = {}, df_dy = {}", df_dx, df_dy);
//convert symbolic expression to a Rust function and evaluate the function
let args = _vec!["_x","_y"];
let function_of_x_and_y = parsed_expression.lambdify( args );
let f_res = function_of_x_and_y( &[1.0, 2.0] );
println!("f_res = {}", f_res);
// or you dont want to pass arguments you can use lambdify_wrapped, arguments will be found inside function
let function_of_x_and_y = parsed_expression.lambdify_wrapped( );
let f_res = function_of_x_and_y( &[1.0, 2.0] );
println!("f_res2 = {}", f_res);
// evaluate function of 2 or more arguments using linspace for defining vectors of arguments
let start = _vec![ 1.0, 1.0];
let end = _vec![ 2.0, 2.0];
let result = parsed_expression.lamdified_from_linspace(start.clone(), end.clone(), 10);
println!("evaluated function of 2 arguments = {:?}", result);
// find _vector of derivatives with respect to all arguments
let vector_of_derivatives = parsed_expression.diff_multi();
println!("vector_of_derivatives = {:?}, {}", vector_of_derivatives, vector_of_derivatives.len());
// compare numerical and analtical derivatives for a given linspace defined by start, end _values and number of _values.
// max_norm - maximum norm of the difference between numerical and analtical derivatives
let comparsion = parsed_expression.compare_num(start, end, 100, 1e-6);
println!(" result_of compare = {:?}", comparsion);
- the same for a function of one variable
// FUNTION OF 1 VARIABLE (processing of them has a slightly easier syntax then for multiple variables)
// function of 1 argument (1D examples)
let input = "log(_x)";
let f = Expr::parse_expression(input);
//convert symbolic expression to a Rust function and evaluate the function
let f_res = f.lambdify1D()(1.0);
let df_dx = f.diff("_x");
println!("df_dx = {}, log(1) = {}", df_dx, f_res);
let input = "_x+exp(_x)";
let f = Expr::parse_expression(input);
let f_res = f.lambdify1D()(1.0);
println!("f_res = {}", f_res);
let start = 0.0;
let end = 10 as f64;
let num_values = 100;
let max_norm = 1e-6;
// compare numerical and analtical derivatives for a given linspace defined by start, end _values and number of _values.
// a norm of the difference between the two of them is returned, and the answer is true if the norm is below max_norm
let (norm, _res) = f.compare_num1D("_x", start, end, num_values, max_norm);
println!("norm = {}, _res = {}", norm, _res);
- a symbolic function can be defined in a more straightforward way without parsing expression
// SOME USEFUL FEATURES
// first define symbolic variables
let vector_of_symbolic_vars = Expr::Symbols( "a, b, c");
println!("vector_of_symbolic_vars = {:?}", vector_of_symbolic_vars);
let (mut a,mut b, mut c) = (vector_of_symbolic_vars[0].clone(),
// consruct symbolic expression
vector_of_symbolic_vars[1].clone(), vector_of_symbolic_vars[2]. clone());
let mut symbolic_expression = a + Expr::exp(b * c);
println!("symbolic_expression = {:?}", symbolic_expression);
// if you want to change a variable inti constant:
let mut expression_with_const = symbolic_expression.set_variable("a", 1.0);
println!("expression_with_const = {:?}", expression_with_const);
let parsed_function = expression_with_const.sym_to_str("a");
println!("{}, sym to string:", parsed_function);
- calculate symbolic jacobian and evaluate it
// JACOBIAN
// instance of Jacobian _structure
let mut Jacobian_instance = Jacobian::new();
// function of 2 or more arguments
let vec_of_expressions = _vec![ "2*_x^3+_y".to_string(), "1.0".to_string()];
// set _vector of functions
Jacobian_instance.set_funcvecor_from_str(vec_of_expressions);
// set _vector of variables
// Jacobian_instance.set_varvecor_from_str("_x, _y");
Jacobian_instance.set_variables(_vec!["_x", "_y"]);
// calculate symbolic jacobian
Jacobian_instance.calc_jacobian();
// transform into human...kind of readable form
Jacobian_instance.readable_jacobian();
// generate jacobian made of regular rust functions
Jacobian_instance.jacobian_generate(_vec!["_x", "_y"]);
println!("Jacobian_instance: functions {:?}. Variables {:?}", Jacobian_instance.vector_of_functions, Jacobian_instance.vector_of_variables);
println!("Jacobian_instance: Jacobian {:?} readable {:?}.", Jacobian_instance.symbolic_jacobian, Jacobian_instance.readable_jacobian);
for _i in 0.. Jacobian_instance.symbolic_jacobian.len() {
for j in 0.. Jacobian_instance.symbolic_jacobian[_i].len() {
println!("Jacobian_instance: Jacobian {} row {} colomn {:?}", _i, j, Jacobian_instance.symbolic_jacobian[_i][j]);
}
}
// calculate element of jacobian (just for control)
let ij_element = Jacobian_instance.calc_ij_element(0, 0, _vec!["_x", "_y"],_vec![10.0, 2.0]) ;
println!("ij_element = {:?} \n", ij_element);
// evaluate jacobian to numerical _values
Jacobian_instance.evaluate_func_jacobian(&_vec![10.0, 2.0]);
println!("Jacobian = {:?} \n", Jacobian_instance.evaluated_jacobian);
// lambdify and evaluate function _vector to numerical _values
Jacobian_instance. lambdify_and_ealuate_funcvector(_vec!["_x", "_y"], _vec![10.0, 2.0]);
println!("function _vector = {:?} \n", Jacobian_instance.evaluated_functions);
// or first lambdify
Jacobian_instance.lambdify_funcvector(_vec!["_x", "_y"]);
// then evaluate
Jacobian_instance.evaluate_funvector_lambdified(_vec![10.0, 2.0]);
println!("function _vector after evaluate_funvector_lambdified = {:?} \n", Jacobian_instance.evaluated_functions);
// evaluate jacobian to nalgebra matrix format
Jacobian_instance.evaluate_func_jacobian_DMatrix(_vec![10.0, 2.0]);
println!("Jacobian_DMatrix = {:?} \n", Jacobian_instance.evaluated_jacobian_DMatrix);
// evaluate function _vector to nalgebra matrix format
Jacobian_instance.evaluate_funvector_lambdified_DVector(_vec![10.0, 2.0]);
println!("function _vector after evaluate_funvector_lambdified_DMatrix = {:?} \n", Jacobian_instance.evaluated_functions_DVector);
- set and calculate the system of (nonlinear) algebraic equations
//use the shortest way to solve system of equations
// first define system of equations and initial guess
let mut NR_instanse = NR::new();
let vec_of_expressions = _vec![ "_x^2+_y^2-10".to_string(), "_x-_y-4".to_string()];
let initial_guess = _vec![1.0, 1.0];
// solve
NR_instanse.eq_generate_from_str(vec_of_expressions,initial_guess, 1e-6, 100, 1e-6);
NR_instanse.solve();
println!("result = {:?} \n", NR_instanse.get_result().unwrap());
// or more verbose way...
// first define system of equations
let vec_of_expressions = _vec![ "_x^2+_y^2-10".to_string(), "_x-_y-4".to_string()];
let mut Jacobian_instance = Jacobian::new();
Jacobian_instance.set_funcvecor_from_str(vec_of_expressions);
Jacobian_instance.set_variables(_vec!["_x", "_y"]);
Jacobian_instance.calc_jacobian();
Jacobian_instance.jacobian_generate(_vec!["_x", "_y"]);
Jacobian_instance.lambdify_funcvector(_vec!["_x", "_y"]);
Jacobian_instance.readable_jacobian();
println!("Jacobian_instance: functions {:?}. Variables {:?}", Jacobian_instance.vector_of_functions, Jacobian_instance.vector_of_variables);
println!("Jacobian_instance: Jacobian {:?} readable {:?}. \n", Jacobian_instance.symbolic_jacobian, Jacobian_instance.readable_jacobian);
let initial_guess = _vec![1.0, 1.0];
// in case you are interested in Jacobian value at initial guess
Jacobian_instance.evaluate_func_jacobian_DMatrix(initial_guess.clone());
Jacobian_instance.evaluate_funvector_lambdified_DVector(initial_guess.clone());
let guess_jacobian = (Jacobian_instance.evaluated_jacobian_DMatrix).clone();
println!("guess Jacobian = {:?} \n", guess_jacobian.try_inverse());
// defining NR method instance and solving
let mut NR_instanse = NR::new();
NR_instanse.set_equation_sysytem(Jacobian_instance, initial_guess, 1e-6, 100, 1e-6);
NR_instanse.solve();
println!("result = {:?} \n", NR_instanse.get_result().unwrap());
- set the system of ordinary differential equations (ODEs), compute the analytical Jacobian ana solve it with BDF method.
//create instance of _structure for symbolic equation system and Jacobian
let mut Jacobian_instance = Jacobian::new();
// define argument andunknown variables
let _x = Expr::Var("_x".to_string()); // argument
let _y = Expr::Var("_y".to_string());
let z:Expr = Expr::Var("z".to_string());
//define equation system
let eq1:Expr = Expr::Const(-1.0 as f64)*z.clone() - (Expr::Const(-1.0 as f64)*_y.clone() ).exp();
let eq2:Expr = _y;
let eq_system = _vec![eq1, eq2];
// set unkown variables
let _values = _vec![ "z".to_string(), "_y".to_string()];
// set argument
let arg = "_x".to_string();
// set method
let method = "BDF".to_string();
// set initial conditions
let t0 = 0.0;
let y0 = _vec![1.0, 1.0];
let t_bound = 1.0;
// set solver parameters (optional)
let first_step = None;
let atol = 1e-5;
let rtol = 1e-5;
let max_step = 1e-3;
let jac_sparsity = None;
let vectorized = false;
// create instance of ODE solver and solve the system
let mut ODE_instance = ODEsolver::new_complex(
eq_system,
_values,
arg,
method,
t0,
y0.into(),
t_bound,
max_step,
rtol,
atol,
jac_sparsity,
vectorized,
first_step
);
// here Jacobian is automatically generated and system is solved
ODE_instance.solve();
// plot the solution (optonally)
ODE_instance.plot_result();
//save results to file (optional)
ODE_instance.save_result();
- the laziest way to solve ODE with BDF
// set RHS of system as _vector of strings
let RHS = _vec!["-z-exp(-_y)", "_y"];
// parse RHS as symbolic expressions
let Equations = Expr::parse_vector_expression(RHS.clone());
let _values = _vec![ "z".to_string(), "_y".to_string()];
println!("Equations = {:?}", Equations);
// set argument
let arg = "_x".to_string();
// set method
let method = "BDF".to_string();
// set initial conditions
let t0 = 0.0;
let y0 = _vec![1.0, 1.0];
let t_bound = 1.0;
// set solver parameters (optional)
let first_step = None;
let atol = 1e-5;
let rtol = 1e-5;
let max_step = 1e-3;
let jac_sparsity = None;
let vectorized = false;
// create instance of ODE solver and solve the system
let mut ODE_instance = ODEsolver::new_complex(
Equations,
_values,
arg,
method,
t0,
y0.into(),
t_bound,
max_step,
rtol,
atol,
jac_sparsity,
vectorized,
first_step
);
ODE_instance.solve();
ODE_instance.plot_result();
- Backward Euler method
// Backward Euler method: slightly non-linear ODE
let RHS = _vec!["-z-exp(-_y)", "_y"];
// parse RHS as symbolic expressions
let Equations = Expr::parse_vector_expression(RHS.clone());
let _values = _vec![ "z".to_string(), "_y".to_string()];
println!("eq_system = {:?}", Equations);
let y0 = DVector::from_vec(_vec![1.0, 1.0]);
let arg = "_x".to_string();
let tolerance = 1e-2;
let max_iterations = 500;
let h = Some(1e-3);// this is the fixed time step version.
// let h = None; - this is the adaptive time step version
let t0 = 0.0;
let t_bound = 1.0;
let mut solver = BE::new();
solver.set_initial( Equations, _values, arg, tolerance, max_iterations, h, t0, t_bound, y0);
println!("_y = {:?}, initial_guess = {:?}", solver.newton._y,solver.newton.initial_guess);
solver.newton.eq_generate();
solver.solve();
let result = solver.get_result();
solver.plot_result();
- Non-stiff methods are also available
//Non-stiff equations: use ODE general api ODEsolver
// RK45 and Dormand-Prince methods are available
let RHS = _vec!["-z-_y", "_y"];
// parse RHS as symbolic expressions
let Equations = Expr::parse_vector_expression(RHS.clone());
let _values = _vec![ "z".to_string(), "_y".to_string()];
println!("Equations = {:?}", Equations);
// set argument
let arg = "_x".to_string();
// set method
let method = "DOPRI".to_string(); // "RK45".to_string();
// set initial conditions
let t0 = 0.0;
let y0 = _vec![1.0, 1.0];
let t_bound = 1.0;
// set solver parameters (optional)
let max_step = 1e-3;
// create instance of ODE solver and solve the system
let mut ODE_instance = ODEsolver::new_easy(
Equations,
_values,
arg,
method,
t0,
y0.into(),
t_bound,
max_step,
);
ODE_instance.solve();
ODE_instance.plot_result();
- Discretization and jacobian for BVP
let RHS = _vec!["-z-_y", "_y"];
// parse RHS as symbolic expressions
let Equations = Expr::parse_vector_expression(RHS.clone());
let _values = _vec![ "z".to_string(), "_y".to_string()];
let arg = "_x".to_string();
let n_steps = 3;
let h = 1e-4;
let BorderConditions = HashMap::from([
("z".to_string(), (0, 1000.0)),
("_y".to_string(), (1, 333.0)),
]);
let Y = _vec![1.0, 1.0, 1.0, 1.0, 1.0, 1.0];
let mut Jacobian_instance = Jacobian::new();
// creating analytic discretized algebraic system, its functional representation, analytic Jacobian matrix and its functional representation
Jacobian_instance.generate_BVP(Equations.clone(), _values.clone(), arg.clone(),0.0,None, Some( n_steps),
Some (h), None, BorderConditions.clone() );
// analytic Jacobian matrix
let J = &Jacobian_instance.symbolic_jacobian;
// its functional representation
let J_func = &Jacobian_instance.function_jacobian_IVP_DMatrix;
// analytic discretized algebraic system,
let F = &Jacobian_instance.vector_of_functions;
// its functional representation
let F_func = &Jacobian_instance.lambdified_functions_IVP_DVector;
let varvect = &Jacobian_instance.vector_of_variables;
println!("_vector of variables {:?}",varvect);
let Ys = DVector::from_vec(Y.clone());
let J_eval1 = J_func(4.0, &Ys);
println!("Jacobian Dense: J_eval = {:?} \n", J_eval1);
// SPARSE JACOBIAN MATRIX with nalgebra (+sparse feature) crate
Jacobian_instance.generate_BVP_CsMatrix(Equations.clone(), _values.clone(), arg.clone(),0.0,None, Some( n_steps),
Some (h), None, BorderConditions.clone());
let J_func3 = &Jacobian_instance.function_jacobian_IVP_CsMatrix;
let J_eval3 = J_func3(4.0, &Ys);
println!("Jacobian Sparse with CsMatrix: J_eval = {:?} \n", J_eval3);
// SPARSE JACOBIAN MATRIX with sprs crate
Jacobian_instance.generate_BVP_CsMat(Equations.clone(), _values.clone(), arg.clone(), 0.0, None,Some( n_steps),
Some (h), None, BorderConditions.clone());
let J_func2: &Box<dyn Fn(f64, &CsVec<f64>) -> CsMat<f64> >= &Jacobian_instance.function_jacobian_IVP_CsMat;
let F_func2 = &Jacobian_instance.lambdified_functions_IVP_CsVec;
let Ys2 = CsVec::new(Y.len(), _vec![0, 1, 2, 3, 4, 5], Y.clone());
println!("Ys = {:?} \n", &Ys2);
let F_eval2 = F_func2(4.0, &Ys2);
println!("F_eval = {:?} \n", F_eval2);
let J_eval2: CsMat<f64> = J_func2(4.0, &Ys2);
println!("Jacobian Sparse with CsMat: J_eval = {:?} \n", J_eval2);
- Boundary Value Problem (BVP) with Newton-Raphson method with "Naive" _flag it means that Jacobian recalculated every iteration
let eq1 = Expr::parse_expression("_y-z");
let eq2 = Expr::parse_expression("-z^2");
let eq_system = _vec![eq1, eq2];
let _values = _vec!["z".to_string(), "_y".to_string()];
let arg = "_x".to_string();
let tolerance = 1e-5;
let max_iterations = 5000;
let max_error = 0.0;
let t0 = 0.0;
let t_end = 1.0;
let n_steps = 200;
let strategy = "Naive".to_string();//
let strategy_params = None;
let method = "Sparse".to_string();// or "Dense"
let _linear_sys_method= None;
let ones = _vec![0.0; _values.len()*n_steps];
let initial_guess: DMatrix<f64> = DMatrix::from_column_slice(_values.len(), n_steps, DVector::from_vec(ones).as_slice());
let mut BorderConditions = HashMap::new();
BorderConditions.insert("z".to_string(), (0 as usize, 1.0 as f64));
BorderConditions.insert("_y".to_string(), (1 as usize, 1.0 as f64));
assert!(&eq_system.len() == &2);
let mut nr = NRBVP::new(eq_system,
initial_guess,
_values,
arg,
BorderConditions, t0, t_end, n_steps,strategy, strategy_params, _linear_sys_method, method, tolerance, max_iterations, max_error);
println!("solving system");
let solution = nr.solve().unwrap();
// println!("result = {:?}", solution);
nr.plot_result();
- Boundary Value Problem (BVP) with Newton-Raphson method with "Frozen" _flag it means that Jacobian recalculated on condition:
Description of strategy (conditoon of recakc)/ key of strategy / value user must provude for strategy
- only first time: / "Frozen_naive" / None
- every m-th time, where m is a parameter of the strategy: / "every_m" / m
- every time when the solution norm greater than a certain threshold A: / "at_high_norm". / A
- when norm of (_i-1) iter multiplied by certain value B(<1) is lower than norm of _i-th iter : /"at_low_speed". / B
- complex - combined strategies 2,3,4 / "complex" / _vec of parameters [m, A, B]
let eq1 = Expr::parse_expression("_y-z");
let eq2 = Expr::parse_expression("-z^2");
let eq_system = _vec![eq1, eq2];
let _values = _vec!["z".to_string(), "_y".to_string()];
let arg = "_x".to_string();
let tolerance = 1e-5;
let max_iterations = 50;
let max_error = 0.0;
let t0 = 0.0;
let t_end = 1.0;
let n_steps = 800; // Dense: 200 -300ms, 400 - 2s, 800 - 22s, 1600 - 2 min,
let strategy = "Frozen".to_string();//
let strategy_params = Some(HashMap::from([("complex".to_string(),
Some(Vec::from( [ 2 as f64, 5.0, 1e-1, ] ))
)]));
/*
or
Some(HashMap::from([("Frozen_naive".to_string(), None)]));
or
Some(HashMap::from([("every_m".to_string(),
Some(Vec::from( [ 5 as f64] ))
)]));
or
Some(HashMap::from([("at_high_morm".to_string(),
Some(Vec::from( [ 5 as f64] ))
)]));
or
Some(HashMap::from([("at_low_speed".to_string(),
Some(Vec::from( [ 1e-2] ))
)]));
or
Some(HashMap::from([("complex".to_string(),
Some(Vec::from( [ 2.0, 5.0, 1e-, ] ))
)]));
*/
let method = "Sparse".to_string();// or "Dense"
let _linear_sys_method = None;
let ones = _vec![0.0; _values.len()*n_steps];
let initial_guess: DMatrix<f64> = DMatrix::from_column_slice(_values.len(), n_steps, DVector::from_vec(ones).as_slice());
let mut BorderConditions = HashMap::new();
BorderConditions.insert("z".to_string(), (0 as usize, 1.0 as f64));
BorderConditions.insert("_y".to_string(), (1 as usize, 1.0 as f64));
assert!(&eq_system.len() == &2);
let mut nr = NRBVP::new(eq_system,
initial_guess,
_values,
arg,
BorderConditions, t0, t_end, n_steps,strategy, strategy_params, _linear_sys_method, method, tolerance, max_iterations, max_error);
println!("solving system");
let solution = nr.solve().unwrap();
// println!("result = {:?}", solution);
nr.plot_result();
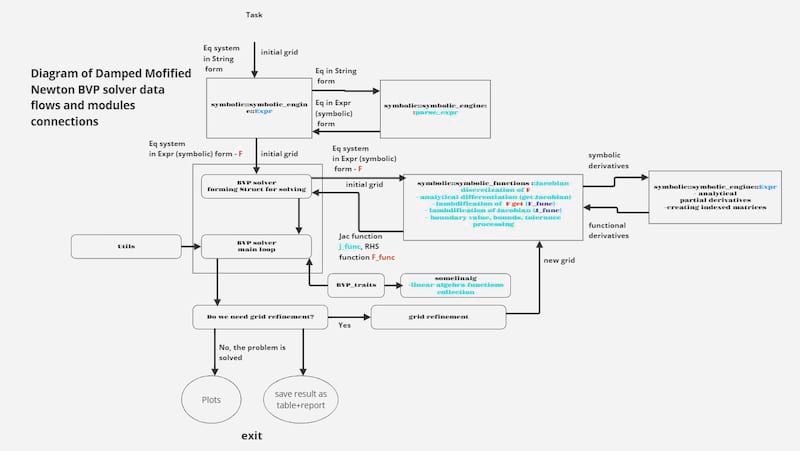
Modified Newton method or Damped Newton method for solving a system of nonlinear ordinary differential equations.
This code implements a modified Newton method for solving a system of non-linear boundary value problems.. The code mostly inspired by sources listed below:
- Cantera MultiNewton solver (MultiNewton.cpp )
- TWOPNT fortran solver (see "The Twopnt Program for Boundary Value Problems" by J. F. Grcar and Chemkin Theory Manual p.261)
A pair of words how to solve BVP problems with the "Damped" feature flag. This algorithm is often used to solve large nonlinear problems.
Let us briefly discuss the "strategy_params" HashMap that defines the solver parameters.
- "max_jac" key: maximum iterations with old Jacobian, None value means the default number is taken-3;
- "maxDampIter" key: maximum number of damped steps, None value means the default value of 5 is used;
- "DampFacor" key: factor to decrease the damping coefficient, None value means the default value of 0.5 is used;
- "adaptive" key: None means no grid refinement is used, if Some - grid refinement is enabled. The first parameter of value vec means what criteria to choose is refinement needed or not in the current iteration, second parameter means maximum number of refinments allowed
Next key-value is optoional and define the name of specific grid refinement algorithm and its parameters;
we recommend to use one of the following algorithms:
- key: "pearson", value: a f64 value less than 1, typically from 0.1 to 0.5;
- key "grcar_smooke" value: a pair of f64 values less than 1, typically first less than second;
if the problem is large and highly nonlinear the best choise is to use the adaptive grid. "We have found that starting the itration on a coarse mesh has several important advntages. One is that the Newton iteration is more likely to converge on a coarse mesh than on a fine mesh. Moreover, the number of variables is small on a coarse mesh and thus the cost per iteration is relatively small. Since the iteration begins from a user-specfied “guess” at the solution, it is likly that many iterations will be required. Ultimately, of course, to be accurate, the solution must be obtained on a fine mesh. However, as the solution is computed on each successively finer mesh, the starting estimates are better, since they come from the converged solution on the previous coarse mesh. In general, the solution on one mesh lies within the domain of convergence of Newton’s method on the next finer mesh.Thus, even though the cost per iteration is increasing, the number of required iterations is decreasing. The adaptve placement of the mesh points to form the finer meshes is done in such a way that the total number of mesh points needed to represent the solution accurately is minimized" Chemkin Theory Manual p.263 So if you choose to use adaptive grid, you should start with the low quantiy of steps (n_steps parameter), grid refinement algorithm will choose the sufficient number of points.
let eq1 = Expr::parse_expression("y-z");
let eq2 = Expr::parse_expression("-z^3");
let eq_system = vec![eq1, eq2];
let values = vec!["z".to_string(), "y".to_string()];
let arg = "x".to_string();
let tolerance = 1e-5;
let max_iterations = 20;
let t0 = 0.0;
let t_end = 1.0;
let n_steps = 100; //
let strategy = "Damped".to_string(); //
let strategy_params = match strategy.as_str() {
"Naive" => None,
"Damped" => Some(HashMap::from([
("max_jac".to_string(), None),// maximum iterations with old Jacobian, None means the default number is taken-3
("maxDampIter".to_string(), None),// maximum number of damped steps, None means the default value of 5 is used
("DampFacor".to_string(), None),// factor to decrease the damping coefficient, None means the default value of 0.5 is used
(
"adaptive".to_string(),// adaptive strategy parameters, None means no grid refinement is used, if Some - grid refinement is enabled
// first parameter means what criteria to choose is refinement needed or not in the current iteration, second parameter means
// maximum number of refinments allowed
Some(vec![1.0, 5.0]), // None
),
// the name of grid refinement strategy, this key-value pair will be used only if "adaptive" is Some, in opposite case this pair
// will be ignored: vector of parametrs is used inside the grid refinement algorithm
// ("pearson".to_string(), Some(vec![0.2] ) ) (""two_point".to_string(), Some(vec![0.2, 0.5, 1.4])),
("two_point".to_string(), Some(vec![0.2, 0.5, 1.4])),
])),
"Frozen" => Some(HashMap::from([(
"every_m".to_string(),
Some(Vec::from([5 as f64])),
)])),
&_ => panic!("Invalid strategy!"),
};
let scheme = "trapezoid".to_string();
let method = "Dense".to_string(); // "Sparse" or "Dense"
let linear_sys_method = None;
let ones = vec![0.0; values.len() * n_steps];
let initial_guess: DMatrix<f64> = DMatrix::from_column_slice(
values.len(),
n_steps,
DVector::from_vec(ones).as_slice(),
);
let mut BorderConditions = HashMap::new();
BorderConditions.insert("z".to_string(), (0usize, 1.0f64));
BorderConditions.insert("y".to_string(), (1usize, 1.0f64));
let Bounds = HashMap::from([
("z".to_string(), (-10.0, 10.0)),
("y".to_string(), (-7.0, 7.0)),
]);
let rel_tolerance = HashMap::from([("z".to_string(), 1e-4), ("y".to_string(), 1e-4)]);
assert_eq!(&eq_system.len(), &2);
let mut nr = BVP::new(
eq_system,
initial_guess,
values,
arg,
BorderConditions,
t0,
t_end,
n_steps,
scheme,
strategy,
strategy_params,
linear_sys_method,
method,
tolerance,
max_iterations,
Some(rel_tolerance),
Some(Bounds),
None, // Some("error".to_string()),Some("warn".to_string()),
);
println!("solving system");
#[allow(unused_variables)]
nr.solve();
// println!("result = {:?}", solution);
// get solution plot using plotters crate or gnuplot crate (gnuplot library MUST BE INSTALLED AND IN THE PATH)
nr.plot_result();
nr.gnuplot_result();
// save to txt, with certain name
nr.save_to_file(None);
// save to csvt, with certain name
nr.save_to_csv(None);
Testing
Our project is covered by tests and you can run them by standard command
cargo test
Contributing
If you have any questions, comments or want to contribute, please feel free to contact us at https://github.com/
To do
- [_x] Write basic functionality
- [_x] Write jacobians
- [_x] Write Newton-Raphson
- [_x] Write BDF
- [_x] Write Backward Euler
- [_x] Write some nonstiff methods
- [_x] Add indexed variables and matrices
- Add more numerical methods for ODEs
- [_x] Add BVP methods for stiff ODEs
Dependencies
~128MB
~2M SLoC