8 releases (breaking)
| 0.8.0 | Mar 16, 2024 |
|---|---|
| 0.7.0 | Mar 15, 2024 |
| 0.6.0 | Mar 15, 2024 |
| 0.5.0 | Mar 12, 2024 |
| 0.1.0 | Mar 2, 2024 |
#420 in Math
63 downloads per month
37KB
790 lines
xensieve
An implementation of the Xenakis Sieve, providing a Sieve from a string expression that filters integer sequences into iterators of integers, Boolean states, or interval widths. Sieves are built from Residuals, defined as a modulus (M) and a shift (S), notated M@S. Sieve string expressions, and Sieve structs, support complementation, intersection, symmetric difference, and union operations on Residuals with operators !, &, ^ and |, respectively.
The Xenakis Sieve is tool for generating discrete interval patterns. Such patterns have boundless applications in creative domains: the Xenakis Sieve can be used to generate scales or multi-octave pitch sequences, rhythms and polyrhythms, and used to control countless other aspects of pictorial or architectural design.
This Rust implementation follows the Python implementation in Ariza (2005), with significant performance and interface enhancements: https://direct.mit.edu/comj/article/29/2/40/93957
Code: https://github.com/flexatone/xensieve-rs
Docs: https://docs.rs/xensieve
Crate: https://crates.io/crates/xensieve
Strategies for Creating Sieves
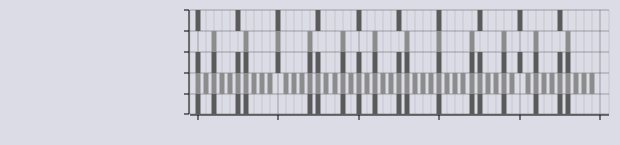
First, we can examine the output of Sieves built from a single Residual. As shown above, a Residual is defined as a modulus (M) and a shift (S), notated M@S. In the diagram below, three Residuals are shown: 5@0, 4@2, and 30@10. As can be seen, for every M units, a value is articulated at the shift S. The final example shows an application of the unary inversion operator !30@10.
Complex Sieves combine Residuals with logical operators such as complementation, intersection, symmetric difference, and union. In the example below, Residuals 5@0 and 4@2 are combined by union with the expression 5@0|4@2. Combining many Residuals by union is a practical approach to building sequences. The final example, (5@0|4@2)&!30@10, shows "removing" selected values from these unioned components by intersecting them with an inverted Residual (!30@10)
While all Sieves are, by definition, periodic, combinations of Residuals can result in sequences with great local complexity and inner patterning.
The xensieve.Sieve Inteface
The Sieves shown above can be created with xensieve.Sieve and used to produce iterators of integers, Boolean states, or interval widths. The Sieve::new constructor accepts arbitrarily complex Sieve expressions.
use xensieve::Sieve;
let s1 = Sieve::new("5@0");
let s2 = Sieve::new("30@10");
let s3 = Sieve::new("(5@0|4@2)&!30@10");
The iter_value() method takes an iterator if integers that can be used to "drive" the Sieve, either with ordered contiguous integers or arbitrary sequences. The iterator yields the subset of integers contained within the Sieve.
use xensieve::Sieve;
assert_eq!(s1.iter_value(0..50).collect::<Vec<_>>(), vec![0, 5, 10, 15, 20, 25, 30, 35, 40, 45]);
assert_eq!(s2.iter_value(0..50).collect::<Vec<_>>(), vec![10, 40]);
assert_eq!(s3.iter_value(0..50).collect::<Vec<_>>(), vec![0, 2, 5, 6, 14, 15, 18, 20, 22, 25, 26, 30, 34, 35, 38, 42, 45, 46]);
The xensieve.Sieve features two alternative iterators to permit using Sieves in different contexts. The iter_state() iterator returns, for each provided integer, the resulting Boolean state.
assert_eq!(s1.iter_state(0..10).collect::<Vec<_>>(), vec![true, false, false, false, false, true, false, false, false, false]);
assert_eq!(s3.iter_state(0..10).collect::<Vec<_>>(), vec![true, false, true, false, false, true, true, false, false, false]);
The iter_interval() iterator returns, for sequential pairs of provided integers that are within the Sieve, the resulting interval.
assert_eq!(s2.iter_interval(0..50).collect::<Vec<_>>(), vec![30]);
assert_eq!(s3.iter_interval(0..50).collect::<Vec<_>>(), vec![2, 3, 1, 8, 1, 3, 2, 2, 3, 1, 4, 4, 1, 3, 4, 3, 1]);
The contains() method can be used to test if arbitrary integers are contained within the Sieve:
assert_eq!(s1.contains(5), true);
assert_eq!(s1.contains(6), false);
assert_eq!(s3.contains(10), false);
assert_eq!(s3.contains(30), true);
What is New in xensieve
0.8.0
Documentation and CI improvements.
0.7.0
Documentation and CI improvements.
0.6.0
CI improvements.
0.5.0
Documentation improvements.
0.4.0
Implemented operator support for &Sieve.
Improved documentation.
0.3.0
Code cleanup and improved doc strings.
0.2.0
Implemented symmetric difference with the ^ operator on Sieve.
0.1.0
First release.