31 releases (15 stable)
| 1.6.0 | Dec 17, 2024 |
|---|---|
| 1.5.0 | Sep 21, 2023 |
| 1.4.0 | Mar 5, 2023 |
| 1.2.6 | Jul 20, 2022 |
| 0.4.1 | Mar 30, 2021 |
#14 in Audio
1,408 downloads per month
Used in 15 crates
(12 directly)
110KB
1.5K
SLoC
Rust: library for frequency spectrum analysis using FFT
An easy to use and fast no_std library (with alloc) to get the frequency
spectrum of a digital signal (e.g. audio) using FFT.
The MSRV (minimum supported Rust version) is 1.63.0.
Supported Platforms
The base library supports all standard and non-standard targets, such as machines running Linux, Ubuntu, Windows, but also embedded systems running custom software.
I want to understand how FFT can be used to get a spectrum
Please see file /EDUCATIONAL.md.
How to use (including no_std-contexts)
Most tips and comments are located inside the code, so please check out the repository on GitHub! Anyway, the most basic usage looks like this:
Cargo.toml
# by default feature "microfft-real" is used
[dependencies]
spectrum-analyzer = "<latest version, see crates.io>"
your_binary.rs
use spectrum_analyzer::{samples_fft_to_spectrum, FrequencyLimit};
use spectrum_analyzer::windows::hann_window;
use spectrum_analyzer::scaling::divide_by_N_sqrt;
/// Minimal example.
fn main() {
// YOU need to implement the samples source; get microphone input for example
let samples: &[f32] = &[0.0, 3.14, 2.718, -1.0, -2.0, -4.0, 7.0, 6.0];
// apply hann window for smoothing; length must be a power of 2 for the FFT
// 2048 is a good starting point with 44100 kHz
let hann_window = hann_window(&samples[0..8]);
// calc spectrum
let spectrum_hann_window = samples_fft_to_spectrum(
// (windowed) samples
&hann_window,
// sampling rate
44100,
// optional frequency limit: e.g. only interested in frequencies 50 <= f <= 150?
FrequencyLimit::All,
// optional scale
Some(÷_by_N_sqrt),
).unwrap();
for (fr, fr_val) in spectrum_hann_window.data().iter() {
println!("{}Hz => {}", fr, fr_val)
}
}
Performance
Measurements taken on i7-1165G7 @ 2.80GHz (Single-threaded) with optimized build
I've tested multiple FFT implementations. Below you can find out why I decided
to use microfft::real. It is not only the fastest, but also works in no_std
contexts.
| Operation | Time |
|---|---|
| Hann Window with 4096 samples | ≈68µs |
| Hamming Window with 4096 samples | ≈118µs |
FFT (rustfft) to spectrum with 4096 samples |
≈170µs |
FFT (microfft::real) to spectrum with 4096 samples |
≈90µs |
FFT (microfft::complex) to spectrum with 4096 samples |
≈250µs |
Example Visualizations
In the following examples you can see a basic visualization of the spectrum from 0 to 4000Hz for
a layered signal of sine waves of 50, 1000, and 3777Hz @ 44100Hz sampling rate. The peaks for the
given frequencies are clearly visible. Each calculation was done with 2048 samples, i.e. ≈46ms of audio signal.
The noise (wrong peaks) also comes from clipping of the added sine waves!
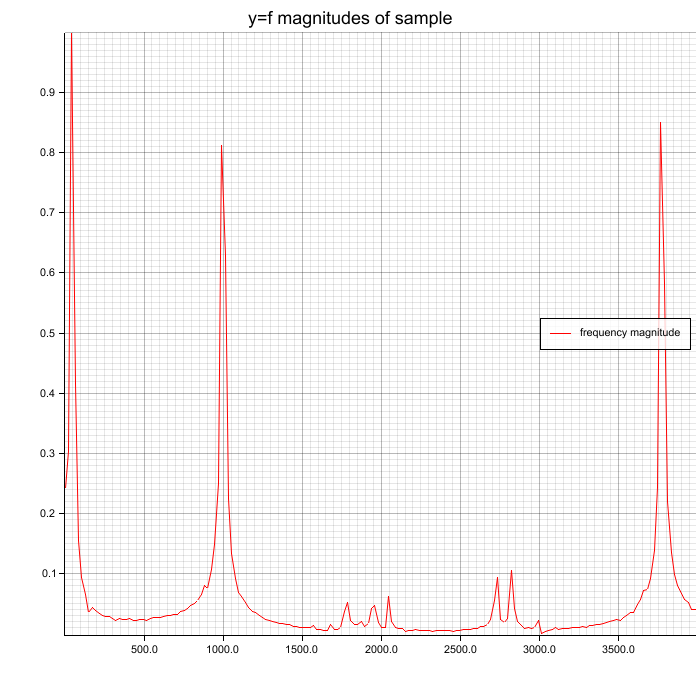
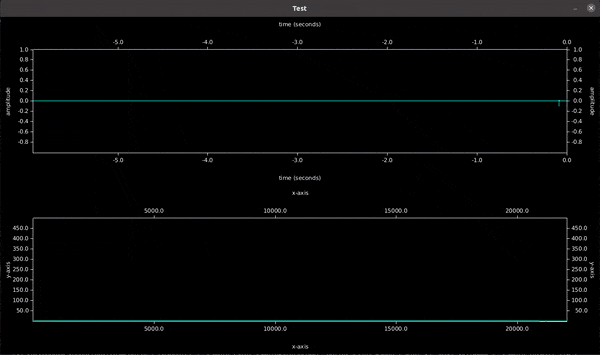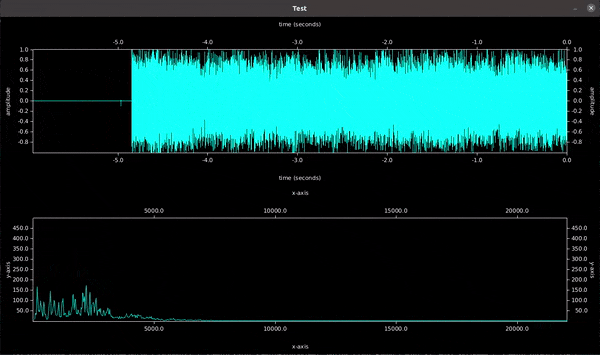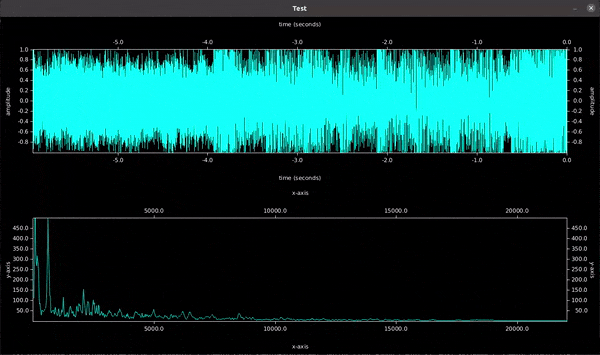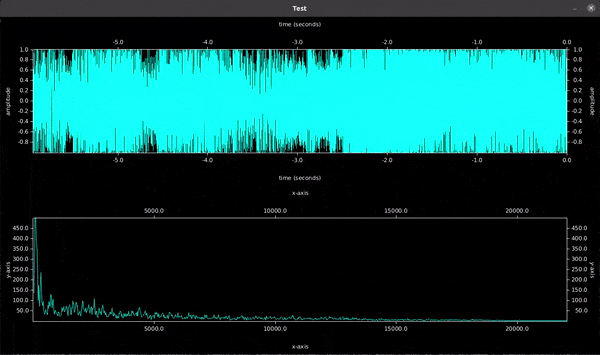
Spectrum without window function on samples
Peaks (50, 1000, 3777 Hz) are clearly visible but also some noise.
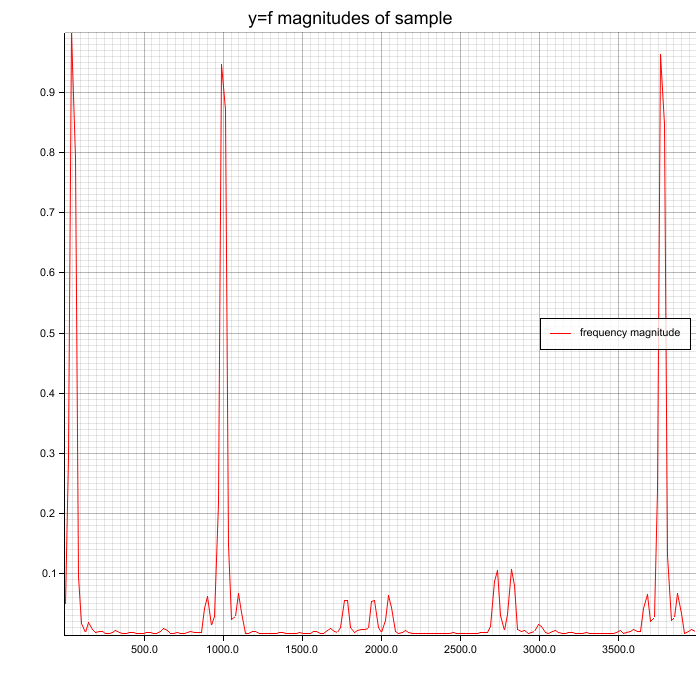
Spectrum with Hann window function on samples before FFT
Peaks (50, 1000, 3777 Hz) are clearly visible and Hann window reduces noise a
little. Because this example has few noise, you don't see much difference.
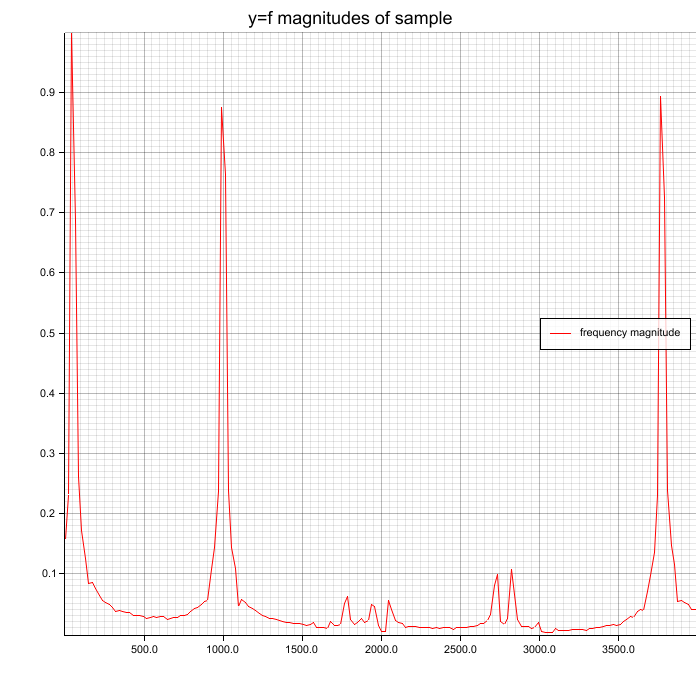
Spectrum with Hamming window function on samples before FFT
Peaks (50, 1000, 3777 Hz) are clearly visible and Hamming window reduces noise a
little. Because this example has few noise, you don't see much difference.
Live Audio + Spectrum Visualization
Execute example $ cargo run --release --example live-visualization. It will
show you how you can visualize audio data in realtime + the current spectrum.
Building and Executing Tests
To execute tests you need the package libfreetype6-dev (on Ubuntu/Debian).
This is required because not all tests are "automatic unit tests" but also tests
that you need to check visually, by looking at the generated diagram of the
spectrum.
Trivia / FAQ
Why f64 and no f32?
I tested f64 but the additional accuracy doesn't pay out the ~40% calculation overhead (on x86_64).
What can I do against the noise?
Apply a window function, like Hann window or Hamming window.
Good resources with more information
- Interpreting FFT Results: https://www.gaussianwaves.com/2015/11/interpreting-fft-results-complex-dft-frequency-bins-and-fftshift/
- FFT basic concepts: https://www.youtube.com/watch?v=z7X6jgFnB6Y
- „The Fundamentals of FFT-Based Signal Analysis and Measurement“ https://www.sjsu.edu/people/burford.furman/docs/me120/FFT_tutorial_NI.pdf
- Fast Fourier Transforms (FFTs) and Windowing: https://www.youtube.com/watch?v=dCeHOf4cJE0
Also check out my blog post.
Dependencies
~2MB
~97K SLoC