7 releases (4 breaking)
| new 0.5.0 | Mar 16, 2025 |
|---|---|
| 0.4.1 | Nov 19, 2024 |
| 0.3.0 | Sep 29, 2024 |
| 0.2.1 | Sep 9, 2024 |
| 0.1.0 | Aug 7, 2024 |
#3 in #educational
124 downloads per month
28MB
4K
SLoC
Table of Contents
- What is an LR(1) parser?
- Why did you make this?
- How can I use the CLI in the picture?
- Can I use it as a standalone library?
- How it works?
- Can I have symbols that can match to empty string?
- Can I have an LALR(1) parser instead of an LR(1) parser?
- What happens if the grammar is ambiguous?
- Any benchmarks?
- Can I modify it?
- Which resources did you use when creating this?
- How is it licensed?
What is an LR(1) parser?
LR(1) parser is a type of bottom-up parser for parsing a subset of context free languages.
1 indicates that the parser will use a single lookahead token when making parsing decisions.
LR(1) parsers are powerful because they can parse a wide range of context free languages, including most programming languages!
Why did you make this?
To learn and to help others learn! This project allows you to visualize LR(1) parsers, from construction to parsing, which makes it easier to understand how they work.
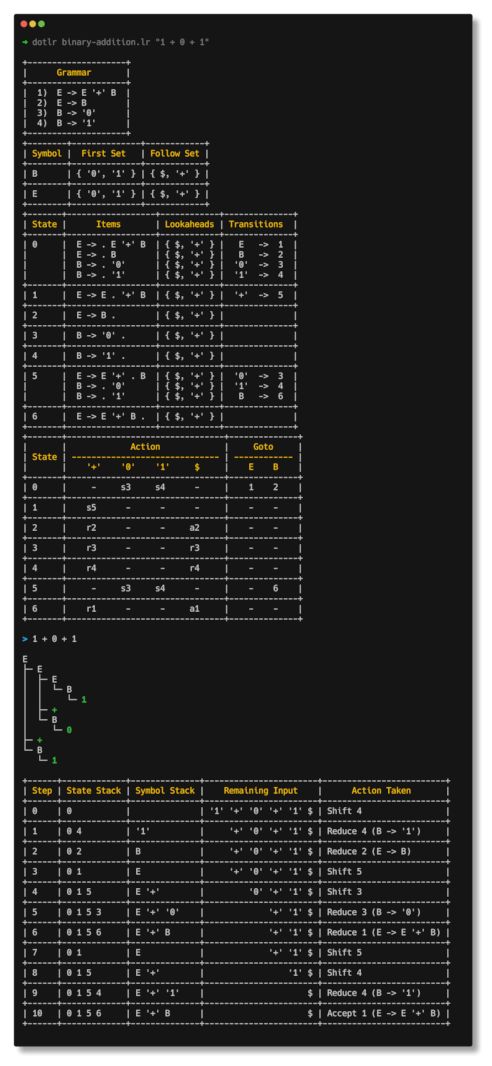
How can I use the CLI in the picture?
If you want to play around with dotlr to visualize parser construction and step-by-step parsing of
different grammars, you can use the main executable of the crate.
Installation
You can install the dotlr cli from crates.io.
cargo install dotlr
Usage
Paste the following into a file called grammar.lr:
P -> E
E -> E '+' T
E -> T
T -> %id '(' E ')'
T -> %id
%id -> /[A-Za-z][A-Za-z0-9]*/
Run dotlr cli with the grammar file and an input:
dotlr grammar.lr "foo(bar + baz)"
It'll print:
+--------------------------------+
| Grammar |
+--------------------------------+
| P -> E |
| E -> E '+' T |
| E -> T |
| T -> %id '(' E ')' |
| T -> %id |
| |
| %id -> /^[A-Za-z][A-Za-z0-9]*/ |
+--------------------------------+
+--------+-----------+-----------------+
| Symbol | First Set | Follow Set |
+--------+-----------+-----------------+
| T | { %id } | { $, '+', ')' } |
+--------+-----------+-----------------+
| E | { %id } | { $, '+', ')' } |
+--------+-----------+-----------------+
| P | { %id } | { $ } |
+--------+-----------+-----------------+
+-------+------------------------+--------------+---------------+
| State | Items | Lookaheads | Transitions |
+-------+------------------------+--------------+---------------+
| 0 | P -> . E | { $ } | E -> 1 |
| | E -> . E '+' T | { $, '+' } | T -> 2 |
| | E -> . T | { $, '+' } | %id -> 3 |
| | T -> . %id '(' E ')' | { $, '+' } | |
| | T -> . %id | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 1 | P -> E . | { $ } | '+' -> 14 |
| | E -> E . '+' T | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 2 | E -> T . | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 3 | T -> %id . '(' E ')' | { $, '+' } | '(' -> 4 |
| | T -> %id . | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 4 | T -> %id '(' . E ')' | { $, '+' } | E -> 5 |
| | E -> . E '+' T | { ')', '+' } | %id -> 6 |
| | E -> . T | { ')', '+' } | T -> 9 |
| | T -> . %id '(' E ')' | { ')', '+' } | |
| | T -> . %id | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 5 | T -> %id '(' E . ')' | { $, '+' } | '+' -> 11 |
| | E -> E . '+' T | { ')', '+' } | ')' -> 13 |
+-------+------------------------+--------------+---------------+
| 6 | T -> %id . '(' E ')' | { ')', '+' } | '(' -> 7 |
| | T -> %id . | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 7 | T -> %id '(' . E ')' | { ')', '+' } | %id -> 6 |
| | E -> . E '+' T | { ')', '+' } | E -> 8 |
| | E -> . T | { ')', '+' } | T -> 9 |
| | T -> . %id '(' E ')' | { ')', '+' } | |
| | T -> . %id | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 8 | T -> %id '(' E . ')' | { ')', '+' } | ')' -> 10 |
| | E -> E . '+' T | { ')', '+' } | '+' -> 11 |
+-------+------------------------+--------------+---------------+
| 9 | E -> T . | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 10 | T -> %id '(' E ')' . | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 11 | E -> E '+' . T | { ')', '+' } | %id -> 6 |
| | T -> . %id '(' E ')' | { ')', '+' } | T -> 12 |
| | T -> . %id | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 12 | E -> E '+' T . | { ')', '+' } | |
+-------+------------------------+--------------+---------------+
| 13 | T -> %id '(' E ')' . | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 14 | E -> E '+' . T | { $, '+' } | %id -> 3 |
| | T -> . %id '(' E ')' | { $, '+' } | T -> 15 |
| | T -> . %id | { $, '+' } | |
+-------+------------------------+--------------+---------------+
| 15 | E -> E '+' T . | { $, '+' } | |
+-------+------------------------+--------------+---------------+
+-------+---------------------------------------+----------------------+
| | Action | Goto |
| State | ------------------------------------- | -------------------- |
| | '+' '(' ')' %id $ | P E T |
+-------+---------------------------------------+----------------------+
| 0 | - - - s3 - | - 1 2 |
+-------+---------------------------------------+----------------------+
| 1 | s14 - - - a1 | - - - |
+-------+---------------------------------------+----------------------+
| 2 | r3 - - - r3 | - - - |
+-------+---------------------------------------+----------------------+
| 3 | r5 s4 - - r5 | - - - |
+-------+---------------------------------------+----------------------+
| 4 | - - - s6 - | - 5 9 |
+-------+---------------------------------------+----------------------+
| 5 | s11 - s13 - - | - - - |
+-------+---------------------------------------+----------------------+
| 6 | r5 s7 r5 - - | - - - |
+-------+---------------------------------------+----------------------+
| 7 | - - - s6 - | - 8 9 |
+-------+---------------------------------------+----------------------+
| 8 | s11 - s10 - - | - - - |
+-------+---------------------------------------+----------------------+
| 9 | r3 - r3 - - | - - - |
+-------+---------------------------------------+----------------------+
| 10 | r4 - r4 - - | - - - |
+-------+---------------------------------------+----------------------+
| 11 | - - - s6 - | - - 12 |
+-------+---------------------------------------+----------------------+
| 12 | r2 - r2 - - | - - - |
+-------+---------------------------------------+----------------------+
| 13 | r4 - - - r4 | - - - |
+-------+---------------------------------------+----------------------+
| 14 | - - - s3 - | - - 15 |
+-------+---------------------------------------+----------------------+
| 15 | r2 - - - r2 | - - - |
+-------+---------------------------------------+----------------------+
> foo(bar + baz)
P
└─ E
└─ T
├─ foo
├─ (
├─ E
│ ├─ E
│ │ └─ T
│ │ └─ bar
│ ├─ +
│ └─ T
│ └─ baz
└─ )
+------+---------------+-------------------+---------------------------+-------------------------------+
| Step | State Stack | Symbol Stack | Remaining Input | Action Taken |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 0 | 0 | | %id '(' %id '+' %id ')' $ | Shift 3 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 1 | 0 3 | %id | '(' %id '+' %id ')' $ | Shift 4 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 2 | 0 3 4 | %id '(' | %id '+' %id ')' $ | Shift 6 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 3 | 0 3 4 6 | %id '(' %id | '+' %id ')' $ | Reduce 4 (T -> %id) |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 4 | 0 3 4 9 | %id '(' T | '+' %id ')' $ | Reduce 2 (E -> T) |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 5 | 0 3 4 5 | %id '(' E | '+' %id ')' $ | Shift 11 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 6 | 0 3 4 5 11 | %id '(' E '+' | %id ')' $ | Shift 6 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 7 | 0 3 4 5 11 6 | %id '(' E '+' %id | ')' $ | Reduce 4 (T -> %id) |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 8 | 0 3 4 5 11 12 | %id '(' E '+' T | ')' $ | Reduce 1 (E -> E '+' T) |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 9 | 0 3 4 5 | %id '(' E | ')' $ | Shift 13 |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 10 | 0 3 4 5 13 | %id '(' E ')' | $ | Reduce 3 (T -> %id '(' E ')') |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 11 | 0 2 | T | $ | Reduce 2 (E -> T) |
+------+---------------+-------------------+---------------------------+-------------------------------+
| 12 | 0 1 | E | $ | Accept 0 (P -> E) |
+------+---------------+-------------------+---------------------------+-------------------------------+
You can also enter REPL mode if you omit the input:
dotlr grammar.lr
Can I use it as a standalone library?
Yes, you can depend on the dotlr crate from crates.io.
Setup
Paste the following to your dependencies section of your Cargo.toml:
dotlr = { version = "0.4", default-features = false }
Example
Here is a basic example that shows the primary operations of the dotlr crate:
use dotlr::{
Grammar,
Parser,
ParserError,
};
const GRAMMAR: &str = r#"
P -> E
E -> E '+' T
E -> T
T -> %id '(' E ')'
T -> %id
%id -> /[A-Za-z][A-Za-z0-9]*/
"#;
const INPUT: &str = r#"
foo(bar + baz)
"#;
fn main() {
let grammar = match Grammar::parse(GRAMMAR.trim()) {
Ok(grammar) => grammar,
Err(error) => {
eprintln!("grammar error: {}", error);
return;
}
};
let parser = match Parser::lr(grammar) {
Ok(parser) => parser,
Err(error) => {
eprintln!("parser error: {}", error);
if let ParserError::Conflict { parser, .. } = error {
parser.dump();
}
return;
}
};
let tokens = match parser.tokenize(INPUT.trim()) {
Ok(tokens) => tokens,
Err(error) => {
eprintln!("tokenization error: {}", error);
return;
}
};
let (parse_trace, parse_tree) = match parser.trace(tokens) {
Ok(result) => result,
Err(error) => {
eprintln!("parsing error: {}", error);
return;
}
};
parser.dump();
println!();
parse_tree.dump();
println!();
parse_trace.dump(parser.grammar());
}
How does it work?
Let's go over a step-by-step construction of the parser for the following grammar:
E -> E '+' F
E -> F
F -> F '*' T
F -> T
T -> %b
%b -> /[0-1]/
And then do a step-by-step explanation of the parsing steps for the following input:
1 + 0 * 1
Few notes before starting:
$represents the end of input tokenεrepresents the empty token
1) Parsing the grammar
First, we need to parse the grammar string to a grammar object that we can work with.
The grammar object will consist of:
-
symbols (HashSet):
- The set of symbols in the grammar
(e.g.,{ E, F, T })
- The set of symbols in the grammar
-
start_symbol (Symbol):
- The symbol to parse
(e.g.,E)
- The symbol to parse
-
empty_symbols (HashSet):
- The set of symbols that can expand to empty string (i.e.,
∀S: S -> '' ∈ rules)
(e.g.,T)
- The set of symbols that can expand to empty string (i.e.,
-
constant_tokens (HashSet):
- The set of constant tokens in the grammar
(e.g.,{ '+', '*' })
- The set of constant tokens in the grammar
-
regular_expressions (HashMap<RegexToken, Regex>):
- The map of regular expression tokens to their corresponding compiled regular expressions
(e.g.,{ b -> /[0-1]/ })
- The map of regular expression tokens to their corresponding compiled regular expressions
-
rules (Vec):
- The list of rules in the grammar
(e.g.,[ E -> E '+' F, E -> F, ... ])
- The list of rules in the grammar
This is done in src/grammar.rs with a simple handwritten parser.
2) Computing FIRST sets
Now, we need to compute a set of tokens for each symbol in the grammar according to the following constraints:
- For each
token ∈ FIRST(Symbol), at least one of the following conditions must hold:-
Symbol -> '' ∈ grammar.rulesandtoken == ε -
Symbol -> (EmptySymbol1 ... EmptySymbolN) ∈ grammar.rulesandtoken == ε -
Symbol -> (EmptySymbol1 ... EmptySymbolN) token ... ∈ grammar.rules -
Symbol -> (EmptySymbol1 ... EmptySymbolN) NonEmptySymbol ... ∈ grammar.rulesandtoken ∈ FIRST(NonEmptySymbol)
-
As for the implementation, here is a python-like pseudocode of the algorithm to compute FIRST sets:
# Start with FIRST(all_symbols) = {}
first_sets = {}
# Iterate until no more changes
while first_sets.has_changed():
# Iterate over the rules of the grammar
for rule in grammar:
# If rule is empty pattern
if rule.is_empty_pattern:
# S -> '' <==> S can start with ε
# -------------------------------
# Add ε to the FIRST set of the symbol of the rule
first_sets[rule.symbol].add(ε)
# Break the processing of the rule as it's fully processed
break
# Iterate over the atoms of the pattern of the rule
for atom in rule.pattern:
# If atom is a token
if atom.is_token:
# S -> (EmptySymbol1 ... EmptySymbolN) '+' ... <==> S can start with '+'
# ----------------------------------------------------------------------
# Add the matching token to the FIRST set of the symbol of the rule
first_sets[rule.symbol].add(atom)
# Break the processing of the rule
# as the rule cannot provide any other first tokens
break
# If atom is a symbol
elif atom.is_symbol:
# S -> (EmptySymbol1 ... EmptySymbolN) E ... <==> S can start with anything E can start with
# ------------------------------------------------------------------------------------------
# Add every token in the FIRST set of the matching symbol
# to the FIRST set of the symbol except ε as it's treated
# in a special way through the loop
first_sets[rule.symbol].extend(first_sets[atom].exclude(ε))
# If the symbol cannot be empty (E -> '' ∉ grammar.rules)
if not atom.can_be_empty:
# Break the processing of the rule
# as the rule cannot provide any other first tokens
break
# If the loop is not broken manually
else:
# S -> EmptySymbol1 ... EmptySymbolN <==> S can start with 'ε'
# -------------------------------------------------------------
# Add ε to the FIRST set of the symbol of the rule
first_sets[rule.symbol].add(ε)
This is done in src/tables.rs.
FIRST sets of the example grammar:
+--------+-----------+
| Symbol | First Set |
+--------+-----------+
| T | { %b } |
+--------+-----------+
| F | { %b } |
+--------+-----------+
| E | { %b } |
+--------+-----------+
3) Computing FOLLOW sets
Next, we need to compute another set of tokens for each symbol in the grammar according the following constraints:
- For each
token ∈ FOLLOW(Symbol), at least one of the following conditions must hold:-
Symbol == grammar.start_symbolandtoken == $ -
Anything -> ... Symbol (EmptySymbol1 ... EmptySymbolN) token ... ∈ grammar.rules -
Anything -> ... Symbol (EmptySymbol1 ... EmptySymbolN) AnotherSymbol ... ∈ grammar.rulesandtoken ∈ FIRST(AnotherSymbol)andtoken != ε -
AnotherSymbol -> ... Symbol (EmptySymbol1 ... EmptySymbolN) ∈ grammar.rulesandtoken ∈ FOLLOW(AnotherSymbol) -
Symbol -> ... AnotherSymbol ∈ grammar.rulesandtoken ∈ FOLLOW(AnotherSymbol)
-
As for the implementation, here is a python-like pseudocode of the algorithm to compute FOLLOW sets:
# Start with just FOLLOW(grammar.start_symbol) = { $ }
follow_sets = { grammar.start_symbol: { $ } }
# Iterate until no more changes
while follow_sets.has_changed():
# Iterate over the rules of the grammar
for rule in grammar:
# Iterate over the atoms of the pattern of the rule
for i in range(len(rule.pattern) - 1):
# If the atom is a symbol
if rule.pattern[i].is_symbol:
# Iterate over the remaining atoms
for j in range(i + 1, len(rule.pattern)):
# If the next atom is a token
if rule.pattern[j].is_token:
# S -> ... E (EmptySymbol1 ... EmptySymbolN) '+' ... <==> E can follow '+'
# ------------------------------------------------------------------------
# Add the matching token to the FOLLOW set of the matching symbol
follow_sets[rule.pattern[i]].add(rule.pattern[j])
# Break the processing of the rule
# as the rule cannot provide any other follow tokens
break
# Or if the next atom is a symbol
elif rule.pattern[j].is_symbol:
# S -> ... E (EmptySymbol1 ... EmptySymbolN) F ... <==> E can follow anything F can start with
# --------------------------------------------------------------------------------------------
# Add every token in the FIRST set of the second symbol
# to the FOLLOW set of the first symbol
# except ε as it's shouldn't be in the follow set
follow_sets[rule.pattern[i]].extend(first_sets[rule.pattern[j]].exclude(ε))
# If the symbol cannot be empty (F -> '' ∉ grammar.rules)
if not rule.pattern[j].can_be_empty:
# Break the processing of the rule
# as the rule cannot provide any other follow tokens
break
# If the loop is not broken manually
else:
# A -> ... S (EmptySymbol1 ... EmptySymbolN) <==> S can follow anything A can follow
# ----------------------------------------------------------------------------------
# Add every token in the FOLLOW set of the symbol of the rule
# to the FOLLOW set of the symbol of the atom
follow_sets[rule.patten[i]].extend(follow_sets[rule.symbol])
# If pattern of ends with a symbol
if rule.pattern[-1].is_symbol:
# S -> ... E <==> S can follow anything E can follow
# --------------------------------------------------
# Add every token in the FOLLOW set of the symbol of the last atom
# to the FOLLOW set of the symbol of the rule
follow_sets[rule.symbol].extend(follow_sets[rule.patten[-1]])
This is done in src/tables.rs.
FOLLOW sets of the example grammar:
+--------+-----------------+
| Symbol | Follow Set |
+--------+-----------------+
| T | { $, '+', '*' } |
+--------+-----------------+
| F | { $, '+', '*' } |
+--------+-----------------+
| E | { $, '+' } |
+--------+-----------------+
4) Constructing the LR(1) automaton
It's time to construct the LR(1) automaton for the grammar.
Here is the drawing of the LR(1) automaton of a different grammar to get an intuition of what an LR(1) automaton is:
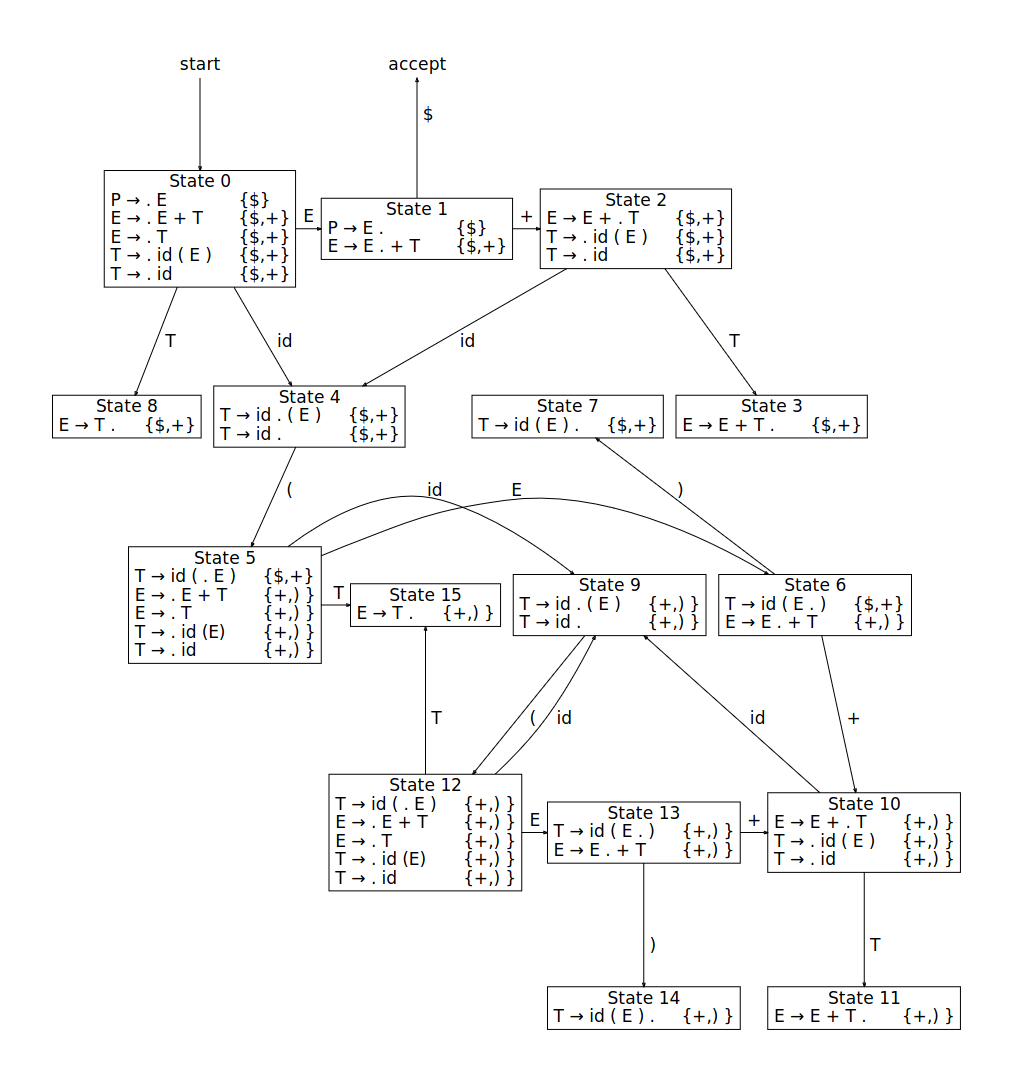
An automaton object is just of a list of states.
Each state has:
-
id (StateId = usize):
- The identifier of the state
(e.g.,0,1)
- The identifier of the state
-
items (Vec):
- The list of LR(1) items of the state
(e.g.,E -> E . '+' F | { $, '+' })
- The list of LR(1) items of the state
-
transitions (HashMap<AtomicPattern, StateId>):
- The map of atomic patterns that would make transition to a new state
(e.g.,{ '+' -> 7 },{ %b -> 4, T -> 6 })
- The map of atomic patterns that would make transition to a new state
Each item has:
-
rule (Rule):
- Underlying rule of the item
(e.g.,E -> E '+' FinE -> E . '+' F | { $, '+' })
- Underlying rule of the item
-
dot (usize):
- Position of the dot in the rule
(e.g.,1inE -> E . '+' F | { $, '+' })
- Position of the dot in the rule
-
lookahead (HashSet):
- The set of tokens that could follow after the rule is applied.
Keep in mind that, one of the lookahead tokens MUST follow for the rule to be applied.
(e.g.,{ $, '+' }inE -> E . '+' F | { $, '+' })
- The set of tokens that could follow after the rule is applied.
Keep in mind that, one of the lookahead tokens MUST follow for the rule to be applied.
As for the implementation, here is a python-like pseudocode of the algorithm to construct the LR(1) automaton:
# Setup the kernel of the first state
first_state = next_empty_state()
for rule in grammar.rules:
if rule.symbol == grammar.start_symbol:
first_state.add_item(Item(rule, dot=0, lookahead={$}))
# Initialize construction state
states_to_process = [first_state]
processed_states = []
# Iterate until there aren't any more states to process.
while len(states_to_process) > 0:
# Get the state to process
state_to_process = states_to_process.pop()
# Computing closure of the state to process
# Loop until no more items are added
while True:
new_items = []
# Iterate current items to obtain new items
for item in state_to_process.items:
# If dot is not at the end of the pattern
if item.dot != len(item.rule.pattern):
# And if there is a symbol after dot
if item.rule.pattern[item.dot].is_symbol:
# Compute the lookahead for the new item
if item.dot == len(item.rule.pattern) - 1:
# S -> ... . E <==> Tokens in the current lookahead can follow E
# --------------------------------------------------------------
lookahead = item.lookahead
elif item.rule.pattern[item.dot + 1].is_token:
# S -> ... . E '+' <==> '+' can follow E
# --------------------------------------
lookahead = {item.rule.pattern[item.dot + 1]}
elif item.rule.pattern[item.dot + 1].is_symbol:
# S -> ... . E F ... <==> Tokens in FIRST(F) can follow E
# -------------------------------------------------------
lookahead = first_sets[item.rule.pattern[item.dot + 1]]
if grammar.can_all_be_empty(item.rule.pattern[item.dot + 1:]):
# S -> ... . E ε ... ε <==> Tokens in the current lookahead can follow E
# S -> ... . E ε ... ε <==> Tokens in FOLLOW(E) can follow E
# ----------------------------------------------------------------------
lookahead = union(
lookahead,
item.lookahead,
follow_sets[item.rule.pattern[item.dot + 1]],
)
# Iterate over the rules of the grammar
for rule in grammar.rules:
# If the rule is for the symbol after dot
if rule.symbol == item.rule.pattern[item.dot]:
# Create a new item from the rule, with dot at the beginning
new_item = Item(rule, dot=0, lookahead=lookahead)
# If the item is not already in items of the state
if new_item not in state_to_process.items:
# Add it the set of new items
new_items.push(new_item)
# Process new items
for new_item in new_items:
# If a similar item with the same rule and the same dot but a different lookahead exists
if state_to_process.has_same_base_item(new_item):
# Merge lookaheads
state_to_process.merge_base_items(new_item)
# Otherwise
else:
# Add the new item directly
state_to_process.items.add(new_item)
# If state hasn't changed, break the loop
if not state_to_process.items.has_changed():
break
# Merge the states to process with an already existing state with the same closure.
replaced = False
for existing_state_with_same_items in processed_states:
if existing_state_with_same_items.items == state_to_process.items:
replaced = True
for state in processed_states:
# Replace transitions from existing states to point to the correct state.
state.transitions.replace_value(state_to_process, existing_state_with_same_items)
break
if replaced:
# If it's merged with an existing state, there is nothing else to do
continue
# Compute transitions of from the state to process.
for item in state_to_process.items:
# If the rule of the items is empty pattern
if item.rule.is_empty_pattern:
# S -> . ε <==> No need to create a transition to item S -> ε .
# --------------------------------------------------------------
continue
# If dot is not at the end
if item.dot == len(item.rule.pattern):
# S -> ... . <==> Can't create a transition as the dot is already at the end
# --------------------------------------------------------------------------
continue
# S -> ... . E ... <==> Seeing E would cause a transition to another state
# S -> ... . '+' ... <==> Seeing '+' would cause a transition to another state
# ----------------------------------------------------------------------------
atomic_pattern_after_dot = item.rule.pattern[item.dot]
# If state to transition is not created yet, create an empty state for it.
if atomic_pattern_after_dot is not in transitions:
# Create an empty state to transition to
state_to_process.transitions[atomic_pattern_after_dot] = next_empty_state()
# Setup the kernel of the state to transition
state_to_transition = state_to_process.transitions[atomic_pattern_after_dot]
state_to_transition.items.push(item.shift_dot_to_right())
# Add state to process to processed states, as we're done with it
processed_states.push(state_to_process)
This is done in src/automaton.rs.
The LR(1) automaton of the example grammar:
+-------+------------------+-----------------+--------------+
| State | Items | Lookaheads | Transitions |
+-------+------------------+-----------------+--------------+
| 0 | E -> . E '+' F | { $, '+' } | E -> 1 |
| | E -> . F | { $, '+' } | F -> 2 |
| | F -> . F '*' T | { $, '+', '*' } | T -> 3 |
| | F -> . T | { $, '+', '*' } | %b -> 4 |
| | T -> . %b | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 1 | E -> E . '+' F | { $, '+' } | '+' -> 7 |
+-------+------------------+-----------------+--------------+
| 2 | E -> F . | { $, '+' } | '*' -> 5 |
| | F -> F . '*' T | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 3 | F -> T . | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 4 | T -> %b . | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 5 | F -> F '*' . T | { $, '+', '*' } | %b -> 4 |
| | T -> . %b | { $, '+', '*' } | T -> 6 |
+-------+------------------+-----------------+--------------+
| 6 | F -> F '*' T . | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 7 | E -> E '+' . F | { $, '+' } | T -> 3 |
| | F -> . F '*' T | { $, '+', '*' } | %b -> 4 |
| | F -> . T | { $, '+', '*' } | F -> 8 |
| | T -> . %b | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
| 8 | E -> E '+' F . | { $, '+' } | '*' -> 5 |
| | F -> F . '*' T | { $, '+', '*' } | |
+-------+------------------+-----------------+--------------+
5) Constructing ACTION and GOTO tables
Finally, we can compute ACTION and GOTO tables of the parser according the following constraints:
-
For each
action ∈ ACTION(state, token), at least one of the following conditions must hold:-
Anything -> ... . token ... | lookahead ∈ state.itemsand
action == Shift(state.transitions[token]) -
Anything -> ... . | lookahead ∈ state.itemsand
token ∈ lookaheadand
token == $and
item.rule.symbol == grammar.start_symboland
action == Accept(item.rule) -
Anything -> . ε | lookahead ∈ state.itemsand
token ∈ lookaheadand
token == $and
item.rule.symbol == grammar.start_symboland
action == Accept(item.rule) -
Anything -> ... . | lookahead ∈ state.itemsand
token ∈ lookaheadand
(token != $oritem.rule.symbol != grammar.start_symbol) and
action == Reduce(item.rule) -
Anything -> . ε | lookahead ∈ state.itemsand
token ∈ lookaheadand
(token != $oritem.rule.symbol != grammar.start_symbol) and
action == Reduce(item.rule)
-
-
For each
goto ∈ GOTO(state, Symbol), at least one of the following conditions must hold:Anything -> ... . Symbol ... | lookahead ∈ state.itemsand
goto == state.transitions[Symbol]
As for the implementation, here is a python-like pseudocode of the algorithm to construct ACTION and GOTO tables:
# Initialize empty action tables
action_table = {}
goto_table = {}
# For each state in the automaton
for state in automaton.states:
# Iterate over the items of the state
for item in state.items:
# If dot is at the end of the item or rule of the item is empty pattern
if item.dot == len(item.rule.pattern) or item.rule.is_empty_pattern:
# S -> ... . <==> We can either reduce the rule or accept if S is a start symbol
# S -> . ε <==> We can either reduce the rule or accept if S is a start symbol
# ------------------------------------------------------------------------------
# We can only perform actions for the tokens in the follow set of the symbol of the rule
for following_token in follow_sets[item.rule.symbol]:
# And only if the token is also in the lookahead of the item
if following_token in item.lookahead:
# Finally, if the token is $ and matching rule is a start symbol
if following_token == $ and item.rule.symbol == grammar.start_symbol:
# We should accept
action_table[state, following_token].push(Accept(item.rule))
# Otherwise
else:
# We should reduce the matching rule
action_table[state, following_token].push(Reduce(item.rule))
else:
# We get the last atomic pattern
atomic_pattern_after_dot = item.rule.pattern[item.dot]
# And the transition on the atomic pattern from the automaton
transition = state.transitions[atomic_pattern_after_dot]
if atomic_pattern_after_dot.is_token:
# S -> ... . '+' ... <==> We should shift and transition to another state
# if the dot precedes a token
# -------------------------------------------------------------------
action_table[state, atomic_pattern_after_dot].push(Shift(transition))
elif atomic_pattern_after_dot.is_symbol:
# S -> ... . E ... <==> We should update GOTO table if the dot precedes a symbol
# This can only happen after a reduction, and the parser
# would look to GOTO table to determine the next state
# --------------------------------------------------------------------------------
goto_table[state, atomic_pattern_after_dot] = transition
This is done in src/tables.rs.
ACTION and GOTO tables of the example grammar:
+-------+-------------------------------+-------------------+
| | Action | Goto |
| State | ----------------------------- | ----------------- |
| | '+' '*' %b $ | E F T |
+-------+-------------------------------+-------------------+
| 0 | - - s4 - | 1 2 3 |
+-------+-------------------------------+-------------------+
| 1 | s7 - - - | - - - |
+-------+-------------------------------+-------------------+
| 2 | r2 s5 - a2 | - - - |
+-------+-------------------------------+-------------------+
| 3 | r4 r4 - r4 | - - - |
+-------+-------------------------------+-------------------+
| 4 | r5 r5 - r5 | - - - |
+-------+-------------------------------+-------------------+
| 5 | - - s4 - | - - 6 |
+-------+-------------------------------+-------------------+
| 6 | r3 r3 - r3 | - - - |
+-------+-------------------------------+-------------------+
| 7 | - - s4 - | - 8 3 |
+-------+-------------------------------+-------------------+
| 8 | r1 s5 - a1 | - - - |
+-------+-------------------------------+-------------------+
6) Tokenizing the input
Tokenization algorithm in dotlr is the simplest tokenization algorithm thinkable.
Here is the idea in a python-like pseudocode:
# Initialize the result
tokens = []
# Loop until all of the input is consumed
remaining_input = input.trim();
while len(remaining_input) > 0:
# Try to match regular expression tokens
for (regex_token, regex) in grammar.regular_expressions:
if match := regex.start_matches(remaining_input):
# We have a match so add it to result
tokens.push(regex_token)
# And shrink remaining input
remaining_input = remaining_input[match.end:].trim()
break
# No regular expression tokens matched
else:
# So try to match constant tokens
for constant_token in grammar.constant_tokens:
if remaining_input.startswith(constant_token):
# We have a match so add it to result
tokens.push(constant_token)
# And shrink remaining input
remaining_input = remaining_input[len(constant_token):]
break
# No tokens matched
else:
raise TokenizationError
# Lastly, add the end of input token so the parser eventually accepts.
tokens.push($)
Tokenized example input:
%b '+' %b '*' %b $
7) Parsing the tokens
Finally, here is the parsing algorithm in a python-like pseudocode:
# Initialize the parsing state
state_stack = [ 0 ]
tree_stack = []
remaining_tokens.reverse()
# Get the first token
current_token = remaining_tokens.pop()
# Loop until algorithm either accepts or rejects
while True:
# Get the current state
current_state = state_stack[-1]
# Get the action to take from ACTION table
action_to_take = action_table[current_state, current_token]
# If the action is to shift
if action_to_take == Shift(next_state):
# Create a terminal tree for the current token and push it to the tree stack
tree_stack.push(TerminalNode(current_token));
# Pop the next token
current_token = remaining_tokens.pop()
# Transition to the next state according to ACTION table
state_stack.push(next_state);
# If the action is to reduce
elif action_to_take == Reduce(rule_index):
# Get the length of the pattern of the rule, say N
rule = grammar.rules[rule_index]
pattern_length = len(rule.pattern)
# Create a non-terminal tree with last N items in the tree stack
tree = NonTerminalNode(rule.symbol, tree_stack[-pattern_length:])
# Shrink state and tree stacks
tree_stack = tree_stack[:-pattern_length]
state_stack = state_stack[:-pattern_length]
# Push the new tree to the tree stack
tree_stack.push(tree)
# Transition to the next state according to GOTO table
state_stack.push(goto_table[state_stack[-1], rule.symbol])
# If the action is to accept
elif action_to_take == Accept(rule_index):
# Create a final non-terminal tree with everything in the tree stack and return it
return NonTerminalNode(grammar.start_symbol, tree_stack)
# No action can be taken, so input is not well-formed
else:
# So raise an error
raise ParsingError
The parsing steps for the example input:
+------+-------------+----------------+--------------------+-------------------------+
| Step | State Stack | Symbol Stack | Remaining Input | Action Taken |
+------+-------------+----------------+--------------------+-------------------------+
| 0 | 0 | | %b '+' %b '*' %b $ | Shift 4 |
+------+-------------+----------------+--------------------+-------------------------+
| 1 | 0 4 | %b | '+' %b '*' %b $ | Reduce 4 (T -> %b) |
+------+-------------+----------------+--------------------+-------------------------+
| 2 | 0 3 | T | '+' %b '*' %b $ | Reduce 3 (F -> T) |
+------+-------------+----------------+--------------------+-------------------------+
| 3 | 0 2 | F | '+' %b '*' %b $ | Reduce 1 (E -> F) |
+------+-------------+----------------+--------------------+-------------------------+
| 4 | 0 1 | E | '+' %b '*' %b $ | Shift 7 |
+------+-------------+----------------+--------------------+-------------------------+
| 5 | 0 1 7 | E '+' | %b '*' %b $ | Shift 4 |
+------+-------------+----------------+--------------------+-------------------------+
| 6 | 0 1 7 4 | E '+' %b | '*' %b $ | Reduce 4 (T -> %b) |
+------+-------------+----------------+--------------------+-------------------------+
| 7 | 0 1 7 3 | E '+' T | '*' %b $ | Reduce 3 (F -> T) |
+------+-------------+----------------+--------------------+-------------------------+
| 8 | 0 1 7 8 | E '+' F | '*' %b $ | Shift 5 |
+------+-------------+----------------+--------------------+-------------------------+
| 9 | 0 1 7 8 5 | E '+' F '*' | %b $ | Shift 4 |
+------+-------------+----------------+--------------------+-------------------------+
| 10 | 0 1 7 8 5 4 | E '+' F '*' %b | $ | Reduce 4 (T -> %b) |
+------+-------------+----------------+--------------------+-------------------------+
| 11 | 0 1 7 8 5 6 | E '+' F '*' T | $ | Reduce 2 (F -> F '*' T) |
+------+-------------+----------------+--------------------+-------------------------+
| 12 | 0 1 7 8 | E '+' F | $ | Accept 0 (E -> E '+' F) |
+------+-------------+----------------+--------------------+-------------------------+
And lastly, the parse tree of the example input:
E
├─ E
│ └─ F
│ └─ T
│ └─ 1
├─ +
└─ F
├─ F
│ └─ T
│ └─ 0
├─ *
└─ T
└─ 1
Can I have symbols that can match to empty string?
Yes, empty symbols are supported!
In the grammar definition, you can have rules like P -> ''
to indicate that P can match the empty string.
P -> 'x' O 'z'
O -> 'y'
O -> ''
When used as the sole pattern, '' will indicate mark the symbol as can be empty.
However, using '' anywhere else would be ignored (e.g., P -> A '' B would be parsed as P -> A B).
The grammar above will be able to parse both x y z and x z.
+----------------------+
| Grammar |
+----------------------+
| 1) P -> 'x' O 'z' |
| 2) O -> 'y' |
| 3) O -> ε |
+----------------------+
+--------+------------+------------+
| Symbol | First Set | Follow Set |
+--------+------------+------------+
| P | { 'x' } | { $ } |
+--------+------------+------------+
| O | { 'y', ε } | { 'z' } |
+--------+------------+------------+
+-------+--------------------+------------+--------------+
| State | Items | Lookaheads | Transitions |
+-------+--------------------+------------+--------------+
| 0 | P -> . 'x' O 'z' | { $ } | 'x' -> 1 |
+-------+--------------------+------------+--------------+
| 1 | P -> 'x' . O 'z' | { $ } | O -> 2 |
| | O -> . 'y' | { 'z' } | 'y' -> 3 |
| | O -> . ε | { 'z' } | |
+-------+--------------------+------------+--------------+
| 2 | P -> 'x' O . 'z' | { $ } | 'z' -> 4 |
+-------+--------------------+------------+--------------+
| 3 | O -> 'y' . | { 'z' } | |
+-------+--------------------+------------+--------------+
| 4 | P -> 'x' O 'z' . | { $ } | |
+-------+--------------------+------------+--------------+
+-------+--------------------------------+--------------+
| | Action | Goto |
| State | ------------------------------ | ------------ |
| | 'x' 'z' 'y' $ | P O |
+-------+--------------------------------+--------------+
| 0 | s1 - - - | - - |
+-------+--------------------------------+--------------+
| 1 | - r3 s3 - | - 2 |
+-------+--------------------------------+--------------+
| 2 | - s4 - - | - - |
+-------+--------------------------------+--------------+
| 3 | - r2 - - | - - |
+-------+--------------------------------+--------------+
| 4 | - - - a1 | - - |
+-------+--------------------------------+--------------+
> x y z
P
├─ x
├─ O
│ └─ y
└─ z
+------+-------------+--------------+-----------------+---------------------------+
| Step | State Stack | Symbol Stack | Remaining Input | Action Taken |
+------+-------------+--------------+-----------------+---------------------------+
| 0 | 0 | | 'x' 'y' 'z' $ | Shift 1 |
+------+-------------+--------------+-----------------+---------------------------+
| 1 | 0 1 | 'x' | 'y' 'z' $ | Shift 3 |
+------+-------------+--------------+-----------------+---------------------------+
| 2 | 0 1 3 | 'x' 'y' | 'z' $ | Reduce 2 (O -> 'y') |
+------+-------------+--------------+-----------------+---------------------------+
| 3 | 0 1 2 | 'x' O | 'z' $ | Shift 4 |
+------+-------------+--------------+-----------------+---------------------------+
| 4 | 0 1 2 4 | 'x' O 'z' | $ | Accept 1 (P -> 'x' O 'z') |
+------+-------------+--------------+-----------------+---------------------------+
> x z
P
├─ x
├─ O
└─ z
+------+-------------+--------------+-----------------+---------------------------+
| Step | State Stack | Symbol Stack | Remaining Input | Action Taken |
+------+-------------+--------------+-----------------+---------------------------+
| 0 | 0 | | 'x' 'z' $ | Shift 1 |
+------+-------------+--------------+-----------------+---------------------------+
| 1 | 0 1 | 'x' | 'z' $ | Reduce 3 (O -> ε) |
+------+-------------+--------------+-----------------+---------------------------+
| 2 | 0 1 2 | 'x' O | 'z' $ | Shift 4 |
+------+-------------+--------------+-----------------+---------------------------+
| 3 | 0 1 2 4 | 'x' O 'z' | $ | Accept 1 (P -> 'x' O 'z') |
+------+-------------+--------------+-----------------+---------------------------+
Can I have an LALR(1) parser instead of an LR(1) parser?
Yes, dotlr supports both LR(1) and LALR(1) parsers!
In the CLI, you can simply use the --lalr option:
dotlr --lalr grammar.lr "1 + 2 * 3"
And in the API, you can use Parser::lalr instead of Parser::lr:
Parser::lalr(grammar)
LALR(1) parser is construction is very similar to LR(1) parser construction. The only difference is that after 4) Constructing the LR(1) automaton, there is another step to reduce the LR(1) automaton to an LALR(1) automaton, using the following algorithm:
# Iterate over the state pairs of the automaton.
for state1 in automaton.states:
for state2 in automaton.states:
# Check if the states share the same core.
# Which means their items are the same ignoring the lookaheads.
# Here is an example:
# ...
# +-------+------------------------+--------------+---------------+
# | 3 | T -> %id . '(' E ')' | { $, '+' } | '(' -> 4 |
# | | T -> %id . | { $, '+' } | |
# +-------+------------------------+--------------+---------------+
# ...
# +-------+------------------------+--------------+---------------+
# | 6 | T -> %id . '(' E ')' | { ')', '+' } | '(' -> 7 |
# | | T -> %id . | { ')', '+' } | |
# +-------+------------------------+--------------+---------------+
# ...
if state1.core == state2.core:
# Merge the states.
# Which is combining lookaheads of the same items.
# Transitions should be mapped to the new states as well.
# Here is the merge of the two states in the example above:
# ...
# +-------+------------------------+-----------------+--------------+
# | 3 | T -> %id . '(' E ')' | { $, '+', ')' } | '(' -> 4 |
# | | T -> %id . | { $, '+', ')' } | |
# +-------+------------------------+-----------------+--------------+
# ...
automaton.merge_states(state1, state2)
the actual implementation is a bit more involved, but the idea is exactly this.
Luckily, it's documented extensively at
automaton.rs
(search for to_lalr). I highly recommend reading the comments in the
source to understand the nuances of the implementation.
What happens if the grammar is ambiguous?
Let's say you want to parse:
1 + 2 * 3
using the grammar:
E -> E '+' E
E -> E '*' E
E -> %int
%int -> /[0-9][1-9]*/
If you create a parser for it, you'll see that it has conflicts:
+------------------------------+
| Grammar |
+------------------------------+
| 1) ^ -> E |
| 2) E -> E '+' E |
| 3) E -> E '*' E |
| 4) E -> %int |
| |
| %int -> /^[0-9][1-9]*/ |
+------------------------------+
+--------+-----------+-----------------+
| Symbol | First Set | Follow Set |
+--------+-----------+-----------------+
| E | { %int } | { $, '+', '*' } |
+--------+-----------+-----------------+
| ^ | { %int } | { $ } |
+--------+-----------+-----------------+
+-------+------------------+-----------------+---------------+
| State | Items | Lookaheads | Transitions |
+-------+------------------+-----------------+---------------+
| 0 | ^ -> . E | { $ } | E -> 1 |
| | E -> . E '+' E | { $, '+', '*' } | %int -> 2 |
| | E -> . E '*' E | { $, '+', '*' } | |
| | E -> . %int | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 1 | ^ -> E . | { $ } | '*' -> 3 |
| | E -> E . '+' E | { $, '+', '*' } | '+' -> 5 |
| | E -> E . '*' E | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 2 | E -> %int . | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 3 | E -> E '*' . E | { $, '+', '*' } | %int -> 2 |
| | E -> . E '+' E | { $, '+', '*' } | E -> 4 |
| | E -> . E '*' E | { $, '+', '*' } | |
| | E -> . %int | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 4 | E -> E '*' E . | { $, '+', '*' } | '*' -> 3 |
| | E -> E . '+' E | { $, '+', '*' } | '+' -> 5 |
| | E -> E . '*' E | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 5 | E -> E '+' . E | { $, '+', '*' } | %int -> 2 |
| | E -> . E '+' E | { $, '+', '*' } | E -> 6 |
| | E -> . E '*' E | { $, '+', '*' } | |
| | E -> . %int | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
| 6 | E -> E '+' E . | { $, '+', '*' } | '*' -> 3 |
| | E -> E . '+' E | { $, '+', '*' } | '+' -> 5 |
| | E -> E . '*' E | { $, '+', '*' } | |
+-------+------------------+-----------------+---------------+
+-------+--------------------------------------------+---------+
| | Action | Goto |
| State | ------------------------------------------ | ------- |
| | '+' '*' %int $ | E |
+-------+--------------------------------------------+---------+
| 0 | - - s2 - | 1 |
+-------+--------------------------------------------+---------+
| 1 | s5 s3 - a | - |
+-------+--------------------------------------------+---------+
| 2 | r4 r4 - r4 | - |
+-------+--------------------------------------------+---------+
| 3 | - - s2 - | 4 |
+-------+--------------------------------------------+---------+
| 4 | r3, s5 r3, s3 - r3 | - |
| | ^^^^^^ ^^^^^^ | |
+-------+--------------------------------------------+---------+
| 5 | - - s2 - | 6 |
+-------+--------------------------------------------+---------+
| 6 | r2, s5 r2, s3 - r2 | - |
| | ^^^^^^ ^^^^^^ | |
+-------+--------------------------------------------+---------+
If we try to parse the input with standard LR, we'll feed tokens one by one and eventually, the parser will be in state 6 with this the symbol stack:
E + E
And the remaining input will be:
* %int $
At this point, the parser could either:
- reduce
E + EtoE - shift
*and transition to state 3 without reductions
This is called a shift-reduce conflict, and it'll result in multiple parse trees:
Parse Tree 1
------------
E
├─ E
│ ├─ E
│ │ └─ 1
│ ├─ +
│ └─ E
│ └─ 2
├─ *
└─ E
└─ 3
Parse Tree 2
------------
E
├─ E
│ └─ 1
├─ +
└─ E
├─ E
│ └─ 2
├─ *
└─ E
└─ 3
(notice that both of these are correct according to the grammar)
Standard LR, can't handle conflicts like this, but there is another algorithm which can: Generalized LR (GLR).
Since v0.5, dotlr has a GLR runtime to support ambiguous grammars! Implementation is based on the
Elkhound paper.
You can think of GLR as standard LR but with multiple state stacks. At each step, GLR parser checks the possible actions that can be performed in each alternative state stack:
- If there are more than one actions, it forks the state stack into multiple new state stacks, obtained by applying one of the actions to each fork.
- If there is a single action, it applies the action to the state stack.
- If there are no actions, it eliminates the state stack.
To be efficient, GLR uses a special data structure called a Graph Structured Stack (GSS). Here is an example:

Red node is something called a GSS top. We can walk it backwards until the root to obtain alternative state stacks:
0 1 3 5 3which has the parse tree of1 + (2 * 3)(E + E)0 1 4 6 3which has the parse tree of(1 + 2) * 3(E * E)0 1 3 5 4 6 3which has the parse tree of1 + 2 * 3(E + E * E)
Because the last stack doesn't have a rule associated with it in the grammar, it'll be eliminated as we accept.
I'd have written a pseudocode for the algorithm, but the
Elkhound paper
does a fantastic job doing that already. Just jump to Figure 7, and enjoy!
Small note, Elkhound has some additional mechanisms to let the user construct/merge parse trees,
but dotlr only constructs its own parse forest, so those parts are slightly different.
To use the GLR runtime in the API, you can use _glr variant of parse and trace methods:
let parse_forest = parser.parse_glr(tokens).expect("failed to parse");
let (parse_trace, parse_forest) = parser.trace_glr(tokens).expect("failed to parse");
To use the GLR runtime in the CLI, you can simply use the --glr option:
dotlr --glr grammar.lr "1 + 2 * 3"
This command will print the two possible parse trees above and then the GLR parse trace:
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| Step | State Stacks | Symbol Stacks | Parse Trees | Remaining Input | Actions Taken | Runtime |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 0 | 0 → | | | %int '+' %int '*' %int $ | From 0 Shift 2 | GLR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 1 | 0 2 ↓ ✗ | %int | 1 | '+' %int '*' %int $ | Via 0 2 Reduce 4 (E -> %int) to 0 1 | GLR |
| | | | | | Eliminate 2 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 2 | 0 1 ↑ → | E | 1 | '+' %int '*' %int $ | From 1 Shift 5 | GLR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 3 | 0 1 5 → | E '+' | 1 + | %int '*' %int $ | From 5 Shift 2 | GLR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 4 | 0 1 5 2 ↓ ✗ | E '+' %int | 1 + 2 | '*' %int $ | Via 5 2 Reduce 4 (E -> %int) to 5 6 | GLR |
| | | | | | Eliminate 2 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 5 | 0 1 5 6 ↑ ↓ | E '+' E | 1 + 2 | '*' %int $ | Via 0 1 5 6 Reduce 2 (E -> E '+' E) to 0 1 | GLR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 6 | 0 1 5 6 → | E '+' E | 1 + 2 | '*' %int $ | From 6 Shift 3 | GLR |
| | 0 1 ↑ → | E | (1 + 2) | | From 1 Shift 3 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 7 | 0 1 5 6 3 → | E '+' E '*' | 1 + 2 * | %int $ | From 3 Shift 2 | GLR |
| | 0 1 3 → | E '*' | (1 + 2) * | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 8 | 0 1 5 6 3 2 ↓ ✗ | E '+' E '*' %int | 1 + 2 * 3 | $ | Via 3 2 Reduce 4 (E -> %int) to 3 4 | GLR |
| | 0 1 3 2 ↓ ✗ | E '*' %int | (1 + 2) * 3 | | Eliminate 2 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 9 | 0 1 5 6 3 4 ↑ ↓ | E '+' E '*' E | 1 + 2 * 3 | $ | Via 5 6 3 4 Reduce 3 (E -> E '*' E) to 5 6 | GLR |
| | 0 1 3 4 ↑ | E '*' E | (1 + 2) * 3 | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 10 | 0 1 5 6 3 4 ✗ | E '+' E '*' E | 1 + 2 * 3 | $ | Via 0 1 3 4 Reduce 3 (E -> E '*' E) to 0 1 | GLR |
| | 0 1 3 4 ↓ ✗ | E '*' E | (1 + 2) * 3 | | Eliminate 4 | |
| | 0 1 5 6 ↑ | E '+' E | 1 + (2 * 3) | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 11 | 0 1 5 6 ↓ ✗ | E '+' E | 1 + (2 * 3) | $ | Via 0 1 5 6 Reduce 2 (E -> E '+' E) to 0 1 | GLR |
| | 0 1 ↑ | E | ((1 + 2) * 3) | | Eliminate 6 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 12 | 0 1 ✔ | E | ((1 + 2) * 3) | $ | In 1 Accept | GLR |
| | 0 1 ↑ ✔ | E | (1 + (2 * 3)) | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
Legend:
- ↓ : reduction is performed along the stack
- ↑ : resulting stack of the reduction from the previous step
- → : current symbol is shifted and a new state is pushed to the stack
- ✗ : stack is eliminated because there were no more reductions from it and it can't shift
- ✔ : stack is accepted and the resulting parse tree is added to the resulting parse forest
Elkhound paper also describes
an LR/GLR hybrid in its Section 3.1, and dotlr implements this hybrid runtime as well!
To use the hybrid runtime in the API, you can use _glr_hybrid variant of parse and trace methods:
let parse_forest = parser.parse_glr_hybrid(tokens).expect("failed to parse");
let (parse_trace, parse_forest) = parser.trace_glr_hybrid(tokens).expect("failed to parse");
To use the hybrid runtime in the CLI, you can simply use the --hybrid option:
dotlr --hybrid grammar.lr "1 + 2 * 3"
This command will also print the same possible parse trees, but the trace will be different:
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| Step | State Stacks | Symbol Stacks | Parse Trees | Remaining Input | Actions Taken | Runtime |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 0 | 0 → | | | %int '+' %int '*' %int $ | From 0 Shift 2 | LR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 1 | 0 2 ↓ | %int | 1 | '+' %int '*' %int $ | Via 0 2 Reduce 4 (E -> %int) to 0 1 | LR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 2 | 0 1 ↑ → | E | 1 | '+' %int '*' %int $ | From 1 Shift 5 | LR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 3 | 0 1 5 → | E '+' | 1 + | %int '*' %int $ | From 5 Shift 2 | LR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 4 | 0 1 5 2 ↓ | E '+' %int | 1 + 2 | '*' %int $ | Via 5 2 Reduce 4 (E -> %int) to 5 6 | LR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 5 | 0 1 5 6 ↑ ↓ | E '+' E | 1 + 2 | '*' %int $ | Via 0 1 5 6 Reduce 2 (E -> E '+' E) to 0 1 | GLR |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 6 | 0 1 5 6 → | E '+' E | 1 + 2 | '*' %int $ | From 6 Shift 3 | GLR |
| | 0 1 ↑ → | E | (1 + 2) | | From 1 Shift 3 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 7 | 0 1 5 6 3 → | E '+' E '*' | 1 + 2 * | %int $ | From 3 Shift 2 | LR |
| | 0 1 3 → | E '*' | (1 + 2) * | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 8 | 0 1 5 6 3 2 ↓ | E '+' E '*' %int | 1 + 2 * 3 | $ | Via 3 2 Reduce 4 (E -> %int) to 3 4 | LR |
| | 0 1 3 2 ↓ | E '*' %int | (1 + 2) * 3 | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 9 | 0 1 5 6 3 4 ↑ ↓ | E '+' E '*' E | 1 + 2 * 3 | $ | Via 5 6 3 4 Reduce 3 (E -> E '*' E) to 5 6 | GLR |
| | 0 1 3 4 ↑ | E '*' E | (1 + 2) * 3 | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 10 | 0 1 5 6 3 4 ✗ | E '+' E '*' E | 1 + 2 * 3 | $ | Via 0 1 3 4 Reduce 3 (E -> E '*' E) to 0 1 | GLR |
| | 0 1 3 4 ↓ ✗ | E '*' E | (1 + 2) * 3 | | Eliminate 4 | |
| | 0 1 5 6 ↑ | E '+' E | 1 + (2 * 3) | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 11 | 0 1 5 6 ↓ ✗ | E '+' E | 1 + (2 * 3) | $ | Via 0 1 5 6 Reduce 2 (E -> E '+' E) to 0 1 | GLR |
| | 0 1 ↑ | E | ((1 + 2) * 3) | | Eliminate 6 | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
| 12 | 0 1 ✔ | E | ((1 + 2) * 3) | $ | In 1 Accept | GLR |
| | 0 1 ↑ ✔ | E | (1 + (2 * 3)) | | | |
+------+-----------------+------------------+----------------+--------------------------+--------------------------------------------+---------+
It's quite similar to the GLR one. The main difference is that in some steps, the runtime is LR.
In those steps, there was only a single top and only a single action that can be performed from
that top. So the hybrid runtime fell back to a faster LR step instead of a standard GLR step.
Please refer to Any benchmarks? section to see how this affects performance.
In the API, glr or hybrid runtimes can be used by
_glr and _glr_hybrid variants of parse and trace methods:
let parse_forest = parser.parse_glr_hybrid(tokens).expect("failed to parse");
let (parse_trace, parse_forest) = parser.trace_glr_hybrid(tokens).expect("failed to parse");
Paper is doing a great job once again explaining how to make it hybrid in Section 3.1, so check it out if you want to learn more.
If you have any questions, feel free to open an issue and we can discuss!
Any benchmarks?
Yes, even though dotlr isn't a performance focused project, I thought it'd be interesting to have
a benchmark suite to see how changes affect its performance, so I've created a couple of JSON
grammars and benchmarked parsing them.
You can run the benchmarks with this command in the project directory:
cargo bench
This command prints the following in my own computer with an Intel i7-12700K CPU:
Parsing JSON / Simple / LR(1) / LR runtime
time: [324.13 ms 324.24 ms 324.36 ms]
thrpt: [76.859 MiB/s 76.888 MiB/s 76.915 MiB/s]
Parsing JSON / Simple / LR(1) / GLR runtime
time: [1.6232 s 1.6337 s 1.6421 s]
thrpt: [15.182 MiB/s 15.260 MiB/s 15.359 MiB/s]
Parsing JSON / Simple / LR(1) / Hybrid runtime
time: [979.79 ms 980.51 ms 981.33 ms]
thrpt: [25.405 MiB/s 25.426 MiB/s 25.445 MiB/s]
Parsing JSON / Simple / LALR(1) / LR runtime
time: [309.04 ms 309.73 ms 310.39 ms]
thrpt: [80.318 MiB/s 80.490 MiB/s 80.669 MiB/s]
Parsing JSON / Simple / LALR(1) / GLR runtime
time: [1.6538 s 1.6591 s 1.6650 s]
thrpt: [14.973 MiB/s 15.026 MiB/s 15.074 MiB/s]
Parsing JSON / Simple / LALR(1) / Hybrid runtime
time: [986.26 ms 986.67 ms 987.15 ms]
thrpt: [25.255 MiB/s 25.267 MiB/s 25.278 MiB/s]
Parsing JSON / Optimized / LR(1) / LR runtime
time: [162.03 ms 162.10 ms 162.17 ms]
thrpt: [153.73 MiB/s 153.80 MiB/s 153.86 MiB/s]
Parsing JSON / Optimized / LR(1) / GLR runtime
time: [1.1012 s 1.1051 s 1.1091 s]
thrpt: [22.479 MiB/s 22.560 MiB/s 22.639 MiB/s]
Parsing JSON / Optimized / LR(1) / Hybrid runtime
time: [709.43 ms 710.10 ms 710.84 ms]
thrpt: [35.072 MiB/s 35.108 MiB/s 35.141 MiB/s]
Parsing JSON / Optimized / LALR(1) / LR runtime
time: [161.90 ms 161.95 ms 162.00 ms]
thrpt: [153.89 MiB/s 153.94 MiB/s 153.99 MiB/s]
Parsing JSON / Optimized / LALR(1) / GLR runtime
time: [1.0918 s 1.0937 s 1.0961 s]
thrpt: [22.745 MiB/s 22.794 MiB/s 22.833 MiB/s]
Parsing JSON / Optimized / LALR(1) / Hybrid runtime
time: [710.09 ms 715.37 ms 721.28 ms]
thrpt: [34.564 MiB/s 34.850 MiB/s 35.109 MiB/s]
Furthermore, it generates an HTML report with detailed plots. You can find this
report at target/criterion/report/index.html, after running the command.
Performance isn't good for a JSON parser, but that's to be expected as it's not the primary objective. Feel free to create pull requests to improve parsing performance, hopefully without changing the understandability of the library.
Also keep in mind that these benchmarks are only for the parsing step. Tokenization is not the focus of this library, and frankly, its implementation is not the best.
Can I modify it?
Of course, feel free to fork dotlr from GitHub, clone the
fork to your machine, fire up your favourite IDE, and make any modification you want.
Don't forget to open up a pull request if you have useful changes that can be beneficial to everyone
using dotlr!
Which resources did you use when creating this?
- https://www3.nd.edu/~dthain/compilerbook/chapter4.pdf
- https://soroushj.github.io/lr1-parser-vis/
- https://jsmachines.sourceforge.net/machines/lr1.html
- https://people.eecs.berkeley.edu/~necula/Papers/elkhound_tr.pdf
How is it licensed?
dotlr is free, open source and permissively licensed!
All code in this repository is dual-licensed under either:
- MIT License (LICENSE-MIT or https://opensource.org/licenses/MIT)
- Apache License, Version 2.0 (LICENSE-APACHE or https://www.apache.org/licenses/LICENSE-2.0)
This means you can select the license you prefer!
Dependencies
~9–19MB
~206K SLoC