28 releases (8 stable)
| 1.5.0 | Jan 10, 2023 |
|---|---|
| 1.4.0 | Dec 26, 2022 |
| 0.3.6 | Dec 21, 2022 |
| 0.2.11 | Dec 20, 2022 |
| 0.0.1 | Dec 7, 2022 |
#1 in #cetkaik
27 downloads per month
Used in 2 crates
5MB
1K
SLoC
cetkaik_compact_representation
机戦の盤面をコンパクトに格納する
前提
0o で始まるものは 8 進数、0b で始まるものは 2 進数
格納方法
まず、以下を「駒番号」とする。
駒番号の上位 2bit は、以下の情報を保持する。
- 上位 2bit が 0b00 → どちらも動かせない(空きマス)
- 上位 2bit が 0b01 → IASideが動かせる(通常駒)
- 上位 2bit が 0b10 → ASideが動かせる(通常駒)
- 上位 2bit が 0b11 → どちらも動かせる(皇)
一方で、通常駒の下位 6bit はゲーム内の全体で unique であり、「盤面から手駒への移動」「手駒から盤面に移動」を経ても下位 6bit は変化しない。
Board
Board は、9 × 9 の二次元配列に、以下の順序で駒情報を詰めたものであり、81 バイトで構成されてアラインメントは 1 である。
[
[KA, LA, ..., PA],
[KE, LE, ..., PE],
...
[KIA, LIA, ..., PIA]
]
初期盤面に対する駒番号の割り当ては、便宜上次のようにする。
[
[0o242, 0o236, 0o226, 0o252, 0o255, 0o253, 0o227, 0o237, 0o243],
[0o247, 0o223, 0o000, 0o233, 0o000, 0o232, 0o000, 0o222, 0o246],
[0o210, 0o211, 0o212, 0o213, 0o257, 0o217, 0o216, 0o215, 0o214],
[0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000],
[0o000, 0o000, 0o000, 0o000, 0o300, 0o000, 0o000, 0o000, 0o000],
[0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000, 0o000],
[0o100, 0o101, 0o102, 0o103, 0o156, 0o107, 0o106, 0o105, 0o104],
[0o144, 0o120, 0o000, 0o130, 0o000, 0o131, 0o000, 0o121, 0o145],
[0o141, 0o135, 0o125, 0o151, 0o154, 0o150, 0o124, 0o134, 0o140],
]
Field
Field は、Board に手駒情報を加えたものであり、手駒情報は 96 ビット(= 12 バイト)のビットベクトルで表される。アラインメントは 1 である。
具体例
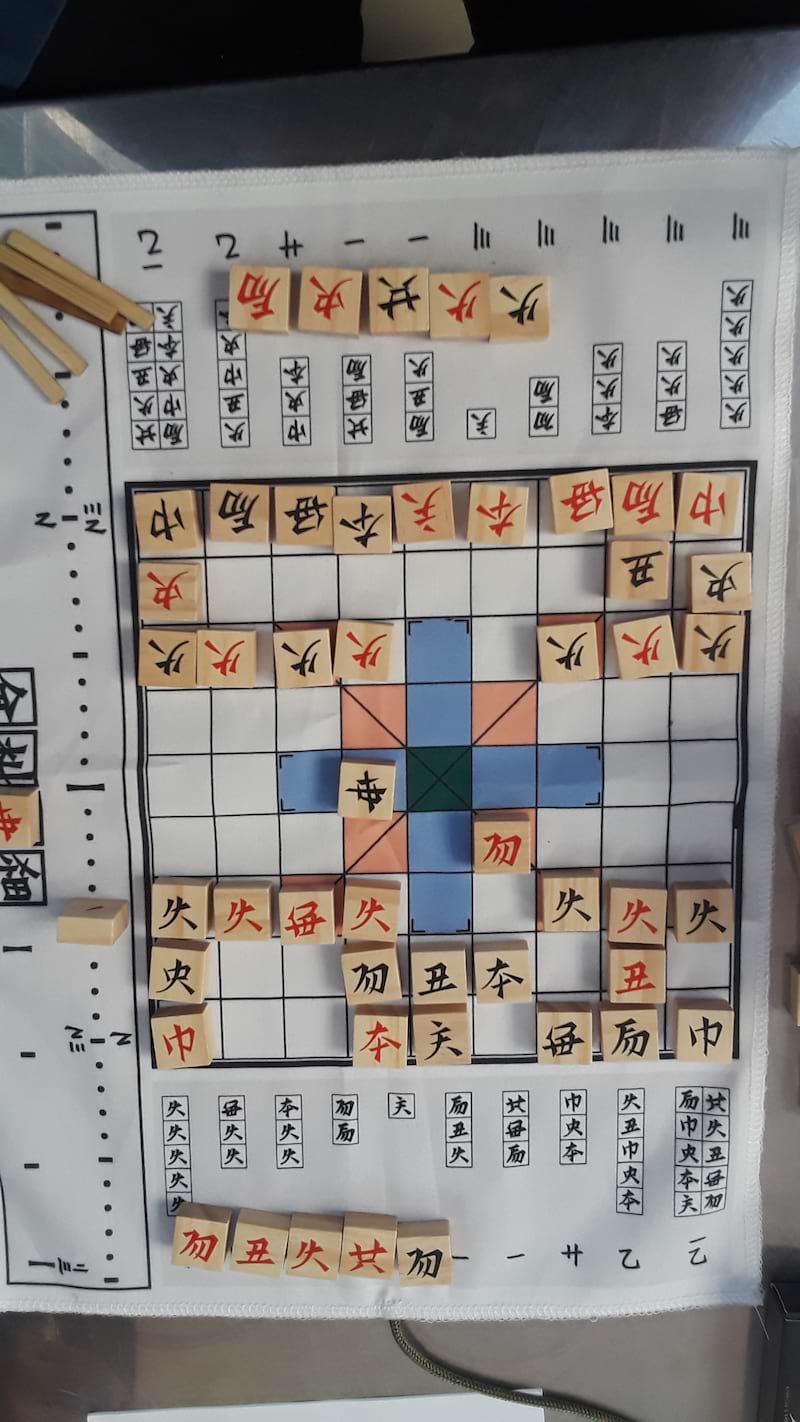
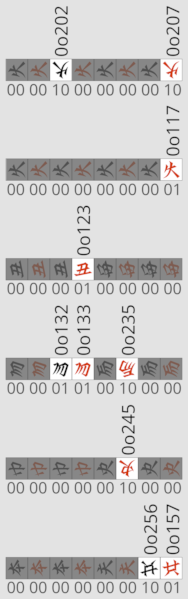
上図では、ASide の赤虎 (0o233)・赤弓 (0o223)・赤兵 (0o217)・赤船 (0o257)・黒虎 (0o232) が IASide の手駒に移っており、IASide の黒兵 (0o102)・赤兵 (0o107)・黒船 (0o156)・赤巫 (0o145)・赤馬 (0o135) が ASide の手駒に移っている。よって、上図をそのままビット列に落とした
[
0b00001000, /* 兵 */ 0b00000010, /* 兵 */
0b00000000, /* 兵 */ 0b00000001, /* 兵 */
0b00000001, /* 弓 */ 0b00000000, /* 車 */
0b00000101, /* 虎 */ 0b00100000, /* 馬 */
0b00000000, /* 筆 */ 0b00100000, /* 巫 */
0b00000000, /* 将 */ 0b00001001 /* 王と船 */
]
が、unsafe { std::mem::transmute::<Hop1zuo1, [u8; 12]>(hop1zuo1) } の結果となる。